Boa noite pessoal!
(Ufal) Pelo uso de certo estacionamento, paga-se 6 reais pela primeira hora, 4 reais pela segunda e 2 reais a cada hora subseqüente. Considere um automóvel que esteve estacionado por H horas (H ? IN*), pelas quais devem ser pagos P reais.
(V) Se H = 1 então P = 6.
(V) Se H = 2 então P = 10.
(V) Se H = 5 então P = 16.
(V) Se H > 2 então P = 2H + 6.
(F) Se H > 2 então P = 2H + 10.
Não entendi porque quando H>2 a função P é P=2H+6, pois a 1ª hora custa 6 reais, e a 2ª hora custa 4 reais, logo o valor fixo, para H>2, é 10 reais (P = 2H+10).
Gostaria que me explicasse isso.
Valeu gente!
para pagar. Mas se você estacionou por 3 horas então deveria pagar 
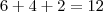, certo?
, desde que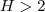 
, isto é 
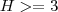. ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
da seguinte forma:
.
da seguinte forma:
.