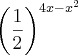
Sei que quanto maior o valor do expoente, menor é o valor da base. E que neste caso o expoente tem de ter um valor positivo (me corrijam se eu estiver errado.). Mas eu não consigo aplicar essas informações no problema.

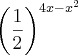

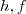 .Donde ,
.Donde , 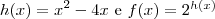 .Assim o menor valor da função f será o minimo absoluto da função h .Então ,
.Assim o menor valor da função f será o minimo absoluto da função h .Então ,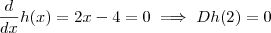 . Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde
. Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde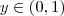

santhiago escreveu:Minha solução :
Considerem as funções.Donde ,
.Assim o menor valor da função f será o minimo absoluto da função h .Então ,
. Como a segunda derivada é maior que zero.Portanto o menor valor da função f será em x = 2 donde
Espero que ajude .

![\left[\frac{1}{2}\right]^{4x -x^2} = 2^{x^2-4x} \left[\frac{1}{2}\right]^{4x -x^2} = 2^{x^2-4x}](/latexrender/pictures/af0ff0c3c944a7b1469cfa536769a1a0.png)
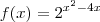 }, onde podemos resscrever que
}, onde podemos resscrever que  .
. cujo objetivo é determinar o menor valor de
cujo objetivo é determinar o menor valor de  .
.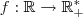 .Assim sabemos que o menor valor da função f estar entre 0 e 1 .
.Assim sabemos que o menor valor da função f estar entre 0 e 1 . precisamos encontar o menor valor da função h .Para isto veja que h é uma função quadrática ,sendo assim podemos encontar menor "valor" pelo vertice da parábola de onde a teoria diz ,
precisamos encontar o menor valor da função h .Para isto veja que h é uma função quadrática ,sendo assim podemos encontar menor "valor" pelo vertice da parábola de onde a teoria diz ,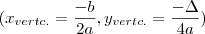 .
.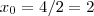 e
e 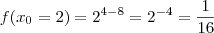 .
.
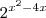 . Note que isto será mínimo quando o expoente for mínimo, pois sabemos que a função exponencial é monotonamente crescente, ou seja, se
. Note que isto será mínimo quando o expoente for mínimo, pois sabemos que a função exponencial é monotonamente crescente, ou seja, se  então
então 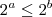 . O mínimo do expoente será o vértice da parábola
. O mínimo do expoente será o vértice da parábola 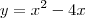 , que acontece em
, que acontece em  , portanto o mínimo será
, portanto o mínimo será 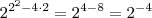 .
.




Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: