 por rhmgh » Dom Ago 12, 2012 21:20
por rhmgh » Dom Ago 12, 2012 21:20
Boa noite galera! será que alguém consegue me ajudar?
Achar a função na forma implícita e na forma cartesiana da função
x=3*cost
y=4*sent
cost=x/3
sent=y/4
cos²t+sen²t=1
(x/3)² + (y/4)² = 1
x²/9 + y²/16 = 1
como que eu avanço? travei nessa parte e não consigo resolver!

-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Seg Ago 13, 2012 08:43
por MarceloFantini » Seg Ago 13, 2012 08:43
A forma cartesiana você já encontrou:
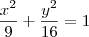
.
A forma implícita é
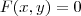
, então tome
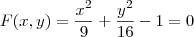
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por rhmgh » Qua Ago 15, 2012 09:30
por rhmgh » Qua Ago 15, 2012 09:30
MarceloFantini escreveu:A forma cartesiana você já encontrou:
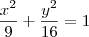
.
A forma implícita é
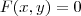
, então tome
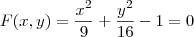
.
ele falo que não da pra fazer assim porque "(x/3)² + (y/4)² = 1" é uma elipse 3 e 4 ai tem que pegar uma função dentro dentro dela e depois isolar o y, mais mesmo assim eu ainda não conseguir ver essa função, consegue me ajudar?
ontem eu tive aula com o prof que deu esse exercício mais ele não quis da a resolução nem a resposta, mas deu essa dica para tentar resolver ...
-
rhmgh
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Dom Jun 10, 2012 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por MarceloFantini » Qua Ago 15, 2012 10:27
por MarceloFantini » Qua Ago 15, 2012 10:27
Não entendo o que ele quer dizer com "pegar uma função dentro dela". É uma elipse sim, que na forma paramétrica é

,
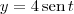
, na forma cartesiana
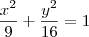
e na forma implícita
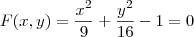
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Função Implicita
por fabriel » Sex Mar 15, 2013 13:27
- 1 Respostas
- 1526 Exibições
- Última mensagem por e8group

Sex Mar 15, 2013 21:50
Cálculo: Limites, Derivadas e Integrais
-
- [derida de função implícita] ajuda ae
por Megatron32 » Ter Set 13, 2011 14:34
- 1 Respostas
- 1078 Exibições
- Última mensagem por LuizAquino

Ter Set 13, 2011 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Função implícita; Questão complicada!
por jemourafer » Qui Mai 17, 2012 18:30
- 4 Respostas
- 4233 Exibições
- Última mensagem por Fabio Wanderley

Sáb Mai 19, 2012 03:16
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Função Implicita-duvidas na resoluão.
por fabriel » Dom Mar 17, 2013 01:11
- 3 Respostas
- 2071 Exibições
- Última mensagem por e8group

Dom Mar 17, 2013 14:39
Cálculo: Limites, Derivadas e Integrais
-
- [Função implícita]não entendi o enunciado do problema.
 por marcosmuscul » Qua Abr 03, 2013 19:09
por marcosmuscul » Qua Abr 03, 2013 19:09
- 3 Respostas
- 2570 Exibições
- Última mensagem por e8group

Qua Abr 03, 2013 20:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




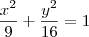 .
.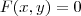 , então tome
, então tome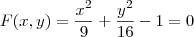 .
.

.
, então tome
.

 ,
, 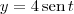 , na forma cartesiana
, na forma cartesiana 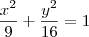 e na forma implícita
e na forma implícita 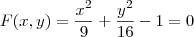 .
.
