Como posso defini-la por ramos?
Será que
é a mesma coisa que 
?
por joaofonseca » Seg Abr 30, 2012 17:13
é a mesma coisa que ?
por MarceloFantini » Sáb Mai 05, 2012 20:59
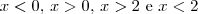. A partir disso, veja a expressão que a função toma e trabalhe disso.
pois, pensando geometricamente, representam a mesma distância ao número dois. Entretanto, como funções, são bem distintas, uma vez que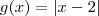 
decresce antes de 2 e cresce a partir dele, enquanto que 
tem o comportamento inverso, crescendo antes deste valor e decrescendo após.
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.