 por Brunaaline » Sex Abr 13, 2012 11:21
por Brunaaline » Sex Abr 13, 2012 11:21
O nivel do anti-ácido no estômago de uma pessoa t minutos após a ingestão de um comprimido anti-ácido é dado por
f(t)= 6t/t²+2t+1
Em que tempo t ocorre o nivel máximo do anti-ácido??
-
Brunaaline
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sex Abr 13, 2012 10:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: biologia
- Andamento: cursando
 por joaofonseca » Sex Abr 13, 2012 16:13
por joaofonseca » Sex Abr 13, 2012 16:13
Em relação à expressão:
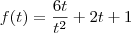
Para encontrar o valor de
t para o qual
f atinge um máximo é necessário encontrar a derivada de
f e depois igualar
f' a zero e resolver. Depois analizar para averiguar se estamos perante um máximo ou minimo.
-
joaofonseca
- Colaborador Voluntário

-
- Mensagens: 196
- Registrado em: Sáb Abr 30, 2011 12:25
- Localização: Lisboa
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funçoes em biologia 2
por Brunaaline » Sex Abr 13, 2012 11:16
- 1 Respostas
- 892 Exibições
- Última mensagem por DanielFerreira

Sex Abr 13, 2012 23:00
Funções
-
- Função em biologia
por Brunaaline » Sex Abr 13, 2012 11:05
- 1 Respostas
- 1553 Exibições
- Última mensagem por DanielFerreira

Sex Abr 13, 2012 22:47
Funções
-
- Probabilidade identidade genética - estudo em biologia
 por pauloadamantino » Sáb Mai 01, 2010 01:56
por pauloadamantino » Sáb Mai 01, 2010 01:56
- 7 Respostas
- 4796 Exibições
- Última mensagem por Elcioschin

Dom Mai 02, 2010 11:14
Estatística
-
- Funções reais. como resolver estas funções...
por LEANDRO HENRIQUE » Ter Mar 04, 2014 18:43
- 0 Respostas
- 3428 Exibições
- Última mensagem por LEANDRO HENRIQUE

Ter Mar 04, 2014 18:43
Funções
-
- [Funções] Domínio e a imagem de funções
 por concurseironf » Qui Ago 21, 2014 12:24
por concurseironf » Qui Ago 21, 2014 12:24
- 1 Respostas
- 4194 Exibições
- Última mensagem por Pessoa Estranha

Sex Ago 22, 2014 20:11
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



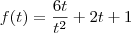

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.