exburro escreveu:Estou tentando resolver esta função
f(x)=x²-|3x+4|
Não faz sentido dizer que você está "tentando resolver esta função".
O que você poderia dizer é que está tentando esboçar o gráfico da função.
exburro escreveu:1. p/ (3x+4)>=0 x>=-4/3
x²-3x+4=0
Errado. Para x >= -4/3 temos que |3x + 4| = 3x + 4. Sendo assim, temos que:
x² - |3x + 4| = x² - (3x + 4) = x² - 3x - 4.
Em resumo: para x >= -4/3 a expressão para a função é x² - 3x - 4.
exburro escreveu:2. p/ (3x+4)<0 x<-4/3
x²+3x-4
Errado. Para x < -4/3 temos que |3x + 4| = -(3x + 4). Sendo assim, temos que:
x² - |3x + 4| = x² - [-(3x + 4)] = x² + 3x + 4.
Em resumo: para x < -4/3 a expressão para a função é x² + 3x + 4.
Juntando o que foi dito nas partes 1. e 2., temos que a função pode ser reescrita como:
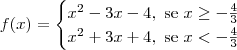
exburro escreveu:Agora eu deveria fazer o gráfico das duas mas tenho a seguinte dúvida... Como vou calcular as raízes se a função 1. terá um delta negativo?
Quando uma função polinomial do segundo grau tem discriminante (delta) negativo, ela
não tem raízes reais e portanto o seu gráfico
não toca o eixo x. O seu gráfico ficará totalmente acima ou totalmente abaixo do eixo x, sendo que ele apenas tocará no eixo y.
Para revisar como construir o gráfico de uma função polinomial do segundo grau, eu recomendo que você assista a videoaula "Matemática - Aula 5 - Função do Segundo Grau". Ela está disponível no canal do Nerckie:
http://www.youtube.com/nerckieAlém disso, vale lembar que a função do exercício é dividida em duas partes. Para cada parte teremos um "pedaço" de parábola. Ou seja, cada parte será um "pedaço" do gráfico de uma função polinomial do segundo grau.


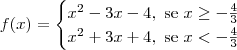

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)