 por Fabricio dalla » Qua Mar 07, 2012 12:54
por Fabricio dalla » Qua Mar 07, 2012 12:54
alguem pode me explicar direito o teorema de bolzano chegui a olhar em um livro e a procurar no site e n entendi muito bem
desde ja agradeço!
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Mar 07, 2012 19:16
por MarceloFantini » Qua Mar 07, 2012 19:16
O teorema de Bolzano diz o seguinte:
Dada uma função contínua

num intervalo fechado
![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png)
, tal que
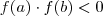
, então existe um
![c \in [a,b] c \in [a,b]](/latexrender/pictures/89a48a2849559c11ee668929aa8a973f.png)
tal que
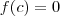
.
Vamos interpretá-lo. Se a função é contínua, então não tem saltos, pontos faltando, etc. Intuitivamente, você pode desenhar o gráfico sem tirar o lápis do papel. A condição de que
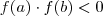
significa que ela muda de sinal, ou seja, ela pode ser positiva e passar a ser negativa ou negativa e passa a ser positiva. A conclusão é que se isto acontece, a função tem uma raíz neste intervalo para algum ponto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercício com Teorema de Bolzano
por fff » Qua Fev 05, 2014 11:54
- 4 Respostas
- 1948 Exibições
- Última mensagem por fff

Qui Fev 06, 2014 17:19
Cálculo: Limites, Derivadas e Integrais
-
- Método da Bissecção Teorema de Bolzano
por romulo39 » Qua Out 12, 2011 00:05
- 1 Respostas
- 1832 Exibições
- Última mensagem por LuizAquino

Qua Out 12, 2011 09:14
Cálculo: Limites, Derivadas e Integrais
-
- Teorema das linhas
por valleska » Seg Mai 18, 2009 21:46
- 1 Respostas
- 3251 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 11:20
Desafios Enviados
-
- teorema de pitagoras
por stanley tiago » Sex Jan 21, 2011 15:59
- 5 Respostas
- 4658 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 15:49
Geometria Analítica
-
- teorema de pitagoras
por stanley tiago » Dom Fev 13, 2011 18:35
- 4 Respostas
- 3496 Exibições
- Última mensagem por stanley tiago

Seg Fev 14, 2011 22:00
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 num intervalo fechado
num intervalo fechado ![[a,b] [a,b]](/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) , tal que
, tal que 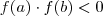 , então existe um
, então existe um ![c \in [a,b] c \in [a,b]](/latexrender/pictures/89a48a2849559c11ee668929aa8a973f.png) tal que
tal que 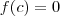 .
. 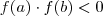 significa que ela muda de sinal, ou seja, ela pode ser positiva e passar a ser negativa ou negativa e passa a ser positiva. A conclusão é que se isto acontece, a função tem uma raíz neste intervalo para algum ponto.
significa que ela muda de sinal, ou seja, ela pode ser positiva e passar a ser negativa ou negativa e passa a ser positiva. A conclusão é que se isto acontece, a função tem uma raíz neste intervalo para algum ponto.
