 por samra » Seg Mar 05, 2012 11:30
por samra » Seg Mar 05, 2012 11:30
Olá gente, bom dia,
Mostre que toda função definida em R (conjunto dos nros reais)
pode ser escrita como uma soma de uma função par com uma função ímpar.Qual raciocínio tenho que usar para fazê-la?
Dei uma olhada nas aulas do Nerckie sobre o assunto, porém la mostra apenas a definição de tais função, assim como a forma de reconhecê-las graficamente.

preciso resolvê-la para hoje a tarde, se alguém puder ajudar-me...

estou lendo assuntos a respeito
se eu conseguir desenvolver o exercício volto aki e coloco pra vocês verem se está certo. Obrigada
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
 por MarceloFantini » Seg Mar 05, 2012 13:25
por MarceloFantini » Seg Mar 05, 2012 13:25
A solução é que para uma função

teremos que
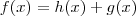
com

, que é par, e

.
Se você fosse encontrar esta decomposição sozinho, vá no rascunho e escreva
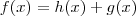
com
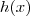
par e

ímpar. Daí,
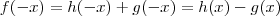
. Agora basta isolar
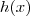
e

, apague o rascunho e faça como eu fiz, apenas dando a resposta final.

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por samra » Sáb Mar 10, 2012 09:55
por samra » Sáb Mar 10, 2012 09:55
Obriigada *-*
^^
"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo] Introdução
por Gabriel_DvT » Sex Mar 30, 2012 11:22
- 1 Respostas
- 1445 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 17:48
Cálculo: Limites, Derivadas e Integrais
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5580 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- Introdução ao cálculo - [Simplificação]
por EDGLE1984 » Seg Ago 18, 2014 13:31
- 1 Respostas
- 1071 Exibições
- Última mensagem por DanielFerreira

Sáb Ago 23, 2014 22:41
Cálculo: Limites, Derivadas e Integrais
-
- funcao impar
por irineu junior » Sex Mar 12, 2010 20:49
- 2 Respostas
- 2565 Exibições
- Última mensagem por irineu junior

Dom Mar 14, 2010 20:55
Funções
-
- Função par x ímpar
por Jonatan » Sex Jul 30, 2010 12:39
- 1 Respostas
- 2365 Exibições
- Última mensagem por Molina

Sex Jul 30, 2010 14:31
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 teremos que
teremos que 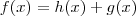 com
com  , que é par, e
, que é par, e  .
.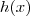 par e
par e  ímpar. Daí,
ímpar. Daí, 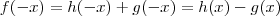 . Agora basta isolar
. Agora basta isolar 


 .
.



