Por exemplo:
1)
![cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}}](/latexrender/pictures/b50d12b10123863eeb4b7ab152fc4d65.png "cos(sen{}^{-1})=\sqrt[]{1-{x}^{2}}")
ou então:
2)
![sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}}](/latexrender/pictures/f44a1203191ba2b62e324ad4720e6ee6.png "sen(tg{}^{-1}x)=\frac{x}{\sqrt[]{1+{x}^{2}}}")
Não entendo essas simplificações. Não sei como chegar aos resultados mostrados.
Peço a quem souber, que me ajude a entender!
por Ana_Rodrigues » Ter Jan 24, 2012 17:46
por LuizAquino » Ter Jan 24, 2012 19:47
Ana_Rodrigues escreveu:1)
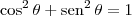
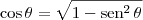(se 
for um ângulo do primeiro ou do quarto quadrante).
. Suponha que ele seja do primeiro ou do quarto quadrante. Temos que: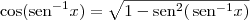
representa a função inversa do seno.
é a função inversa de f, então é válida a propriedade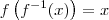 
.
.![\cos (\textrm{sen}^{-1} x) = \sqrt{1 - \left[\textrm{sen} (\,\textrm{sen}^{-1} x)\right]^2} = \sqrt{1-x^2}](/latexrender/pictures/ed9fac86e2c1b54be281083c16654d9c.png "\cos (\textrm{sen}^{-1} x) = \sqrt{1 - \left[\textrm{sen} (\,\textrm{sen}^{-1} x)\right]^2} = \sqrt{1-x^2}")
Ana_Rodrigues escreveu:2)
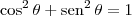e 
podemos obter que: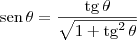
(se for um ângulo do primeiro ou do terceiro quadrante).
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
.
:
![\cos(\textrm{sen}^{-1}\, x)=\sqrt[]{1-{x}^{2}}](/latexrender/pictures/f02af85cefa241ba4977c7f25b5ee88f.png "\cos(\textrm{sen}^{-1}\, x)=\sqrt[]{1-{x}^{2}}")
