Eu fiz assim:
Na expressão que indcas-te, 1 e 9 são zeros da função.
O eixo de simetria da parabola é:
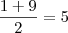
Cinco é a abcissa do vertice da parabola.No enunciado é indicado que 80 é um máximo, logo a parabola está virada para baixo.
Agora subtitui-se
x por 5 na equação a(x - 1)(x - 9)=80 e resolve-se em ordem a
a.
a=-5.
Teste:
Substitui-se
a por -5, e coloca-se a expressão na forma canonica.
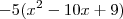
Agora completa-se o trinomio do quadrado perfeito:

Coordenadas do vertice=(5,80).Em relação ao
a, 5 é um fator de expanção vertical e o sinal negativo é o fator de refleção em relação ao eixo Ox.
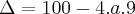


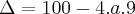


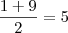
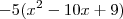




 .
.



