Gente, to com uma grande duvida em um exercicio de equacao modular. se alguem puder me ajudar ficarei grato .. (desculpe se eu estiver postando em local errado, pois sou novo nesse forum)
o exercicio é esse, to com dificuldades pra começar a resolver ele, pelo fato do mesmo ter fracao no modulo ..
|10 -x/2| = 5
x/2 = x sobre 2 HEHE Fracao rs
Aguardo respostas
Obrigado
Renan



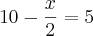

 ou
ou 
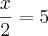

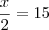

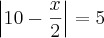 é S = {10 ; 30}
é S = {10 ; 30}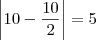
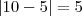
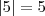 (A igualdade é verdadeira)
(A igualdade é verdadeira)

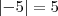 (A igualdade é verdadeira)
(A igualdade é verdadeira) em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.