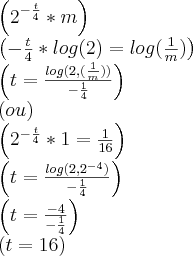por jamiel » Ter Jun 28, 2011 01:25
por jamiel » Ter Jun 28, 2011 01:25
A meia vida do palácio-100 é de quatro dias.( Assim, a metade de qualquer quantidade de Pd 100 vai se desintegrar em 4 dias) . A massa inicial de uma amostra é 1 grama.
a) Encontre a massa restante após 16 dias;
b) Encontre a massa m(t) após t dias
c) Encontre a função inversa de m(t) e explique seu significado
d) Quando a massa ficará reduzida a 0,01 g?
a)

b)

c)
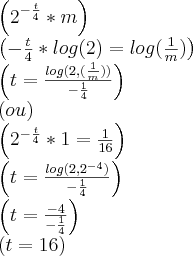
d)

Se alguém puder me ajudar nesta questão também, eu agradeço. Mais uma vez, dúvida com a inversa!
-
jamiel
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Jan 31, 2011 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Mecânica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida Função
por RJ1572 » Qui Abr 08, 2010 23:22
- 3 Respostas
- 2171 Exibições
- Última mensagem por Elcioschin

Sex Abr 09, 2010 13:22
Funções
-
- Dúvida Função
por vb_evan » Sáb Jul 03, 2010 09:18
- 4 Respostas
- 2704 Exibições
- Última mensagem por vb_evan

Qua Jul 07, 2010 09:35
Funções
-
- Função - puc-mg dúvida
por gustavoluiss » Sáb Jan 08, 2011 17:07
- 10 Respostas
- 5359 Exibições
- Última mensagem por Renato_RJ

Sáb Jan 08, 2011 22:49
Funções
-
- Duvida no zero da função
por igorcalfe » Sex Mar 11, 2011 18:14
- 2 Respostas
- 1808 Exibições
- Última mensagem por igorcalfe

Ter Mar 15, 2011 23:35
Sistemas de Equações
-
- Função - Exp e Log - Dúvida!
por jamiel » Seg Jun 27, 2011 23:55
- 0 Respostas
- 5756 Exibições
- Última mensagem por jamiel

Seg Jun 27, 2011 23:55
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.