 por natanskt » Sex Out 22, 2010 20:17
por natanskt » Sex Out 22, 2010 20:17
o VERTICE DA parabola correspondende a função
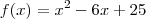
esta associado ao par:
a-)(0,25)
b-)(-1,32)
c-)(1,20)
d-)(-2,52)
e-)(3,16)
essa conta é facil,mais eu faço tudo certo e o resultado não bate,por favor pode fazer a conta pra ver se eu estou errado?
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por DanielRJ » Sex Out 22, 2010 22:14
por DanielRJ » Sex Out 22, 2010 22:14
natanskt escreveu:o VERTICE DA parabola correspondende a função
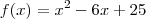
esta associado ao par:
a-)(0,25)
b-)(-1,32)
c-)(1,20)
d-)(-2,52)
e-)(3,16)
essa conta é facil,mais eu faço tudo certo e o resultado não bate,por favor pode fazer a conta pra ver se eu estou errado?
cara meu deus tem que estudar mais...o vertice da função é definido pelo par(xv:yv):
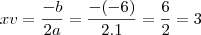
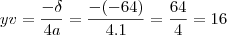
resposta:(3;16)
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (EPCAR)função do 2 grau
por natanskt » Sex Out 22, 2010 11:59
- 1 Respostas
- 2009 Exibições
- Última mensagem por MarceloFantini

Sex Out 22, 2010 15:15
Funções
-
- (EPCAR)função
por natanskt » Sex Out 15, 2010 23:59
- 1 Respostas
- 1351 Exibições
- Última mensagem por Elcioschin

Sáb Out 16, 2010 18:56
Funções
-
- (EPCAR)função
por natanskt » Ter Out 19, 2010 10:31
- 1 Respostas
- 2180 Exibições
- Última mensagem por MarceloFantini

Ter Out 19, 2010 17:49
Funções
-
- [Função]Questão da EPCAR
por -daniel15asv » Sex Ago 03, 2012 16:28
- 1 Respostas
- 4212 Exibições
- Última mensagem por -daniel15asv

Sáb Ago 04, 2012 15:19
Funções
-
- (EPCAR)conjuntos
por natanskt » Sex Out 15, 2010 18:18
- 3 Respostas
- 2095 Exibições
- Última mensagem por DanielRJ

Sex Out 15, 2010 23:07
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
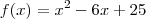 esta associado ao par:
esta associado ao par:
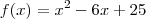 esta associado ao par:
esta associado ao par:
esta associado ao par:
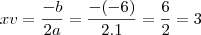
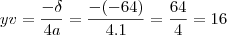


 .
.
 :
: