Ajuda com alguns exercícios

por **Thiago Silveira** » Seg Set 06, 2010 22:18

Pessoal, to fazendo alguns exercícios aqui de funções exponenciais e tive algumas dúvidas, se alguem puder me ajudar, agradeço desde já. Vo colocar tb o que eu tentei fazer...xD
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
1-Duas populações, designadas por F e G, têm os respectivos crescimentos expressos por f(t)=36+t^2

e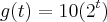

, sendo t número não negativo que representa o tempo em meses. Então analise as seguinte afirmações:
I. A população G duplica a cada mês.
II. g(51)-g(50)=g(50)
III. Quando t=1, a população F é menor do que a população G
IV. Em nenhum momento a população F será igual à população G

Marque a alternativa correta:

a)as afirmações I, II, e IV são corretas.
b)as afirmações I, III e IV são corretas.
c)as afirmações I, II são corretas.
d)as afirmações I e IV são corretas.

O que eu fiz:

Consegui provar q a I e II são verdadeiras, e que III é falsa, mas a IV eu tive duvidas. Nela eu fiz o seguinte: igualei f(t) com g(t) e ficou assim: 36+t^2=10(2^t)

, mas agora eu não sei mais o que fazer, não sei resolver uma equação quadrática com uma exponencial.

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
2- O cuidado com a conservação de alimentos é sempre importante. Uma maionese malconservada causou mal-estar nos frequentadores de um restaurante. Uma investigação revelou a presença de uma bacteria que se multiplica segundo a lei: n(t)=200.2^a^t

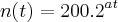em que n(t) é o nº de bacterias encotnradas na amostrada de maionese t horas após o inicio do almoço e a é uma constante real.
O número de bacterias após 1 dia de realização do almoço é, aproximadamente: (Use 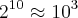$2^1^0 \approx 10^3$ )

a) 0,3 * 10^7

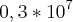
b)

c)

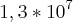
d)

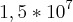
O que eu fiz:
Primeiro que a questão tinha mais duas questões antes. Uma pra calcular o nº inicial de bacterias que é 200. E outra perguntando o valor da constante a dando t=3 e nº de bacterias=800, e achei a=2/3. Essas eu fiz. Agora essa ultima eu consegui calcular, somente converti 1 dia pra horas e joguei na formula e ficou assim:
$n(t)=200*2^{\frac{2}{3}}*2^t$
Agora não sei mais o que fazer. Só desmembrei o 200 e ficou assim: $n(t)=2^3*5^2*2^{\frac{2}{3}}*2^t$

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
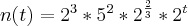
3- A sentença 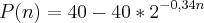$P(n)=40-40*2^{-0,34n}$ permite calcular o número de artigos que um opérario recem-contratado é capaz de produzir diariamente após n dias de treinamento. Para que esse operário produza pelo menos 30 artigos por dia, o menor valor inteiro de n é
a)5
b)6
c)4
d)3
O que eu fiz:
Só joguei o valor 30 na função:
$P(n)=40-40*2^{-0,34n}$
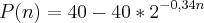
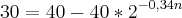
$30=40-40*2^{-0,34n}$
$30-40=-40*2^{-0,34n}$
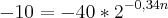
$-10=-40*2^{-0,34n}$
$-10=-40*2^{-0,34n} *(-1)$
$\frac{10}{40}=2^{-0,34n}$
$\frac{1}{4}=2^{-0,34n}$
$2^{-2}=2^{-0,34n}$
-2=-0,34n

$n=\frac{-0,34}{-2}$
n=0,17

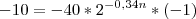
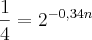
cheguei a isso ai mas nao encontrei resposta.
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
4- A expressão a seguir é equivalente a:

$3^0-\frac{4^\frac{1}{2}}{\frac{1}{2^{-1}}-\frac{1}{5^0-3^{-1}}}$

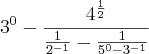
a)-3
b)-2
c)3
d)2

O que eu fiz: fiz mas encontrei 1/2, portanto errei, pq nao tem isso ai nao.

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
5- Efetuando as operações a seguir temos:
$\frac{10*0,0001+0,2*10^{-3}}{0,005}-\frac{0,004*3*10^{-5}}{0,0005*10^{-3}}$

a)100
b)2,4
c)1
d)0
O que eu fiz:
Fui tirando as potencias e deixando alguns numero mas tb não achei nada que esteja alternativas.

---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
6- O valor de x que soluciona esta equação é:

$3^{x-2}=\frac{\sqrt[]{3^4*\sqrt[]{3}}}{27^2*\sqrt[]{3}}$

a)-31/12
b)-7/12
c)-7/12
d)-5/8
e)-9/4

O que eu fiz:
Primeiro que tem duas alternativas iguais :-P

, mas eu fiz e encontrei 10/3, ou seja nenhuma das alternativas.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
7- A equação 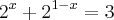$2^x + 2^{1-x}=3$ tem duas raizes reais. O produto delas é:

a)-1
b)0
c)1
d)2

O que eu fiz:
Fiz foi nada nesta. Esse 3 me encucou, aí nao sabia fazer. Pensei até em Girard dividir c/a mas nao deu certo.
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
8- O triplo do valor de x que satisfaz a equação a seguir é

$\frac{4^{\frac{x}{2}}}{2}-\frac{2^{x-1}}{3}=\frac{4}{3}$

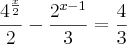
a)2
b)6
c)0
d)9
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Isso aí pessoal, tenho essas questões ai que nao consegui fazer. Queria perguntar uma outra coisa tb. Se alguem pudesse me passar o msn pra poder me ajudar na matemática, pq to com dificuldade em resolver exercício de alguns vestibulares. Agradeço desde já.

Ajuda com alguns exercícios

Ajuda com alguns exercícios

Ajuda com alguns exercícios

Quem está online