 por barizom » Sáb Mar 27, 2010 13:58
por barizom » Sáb Mar 27, 2010 13:58
O enunciado pede para encontrar o dominio da função.

A respota é: D(f)= x pertence aos reais tal que -9 maior ou igual a X e menor que 1.
Consegui achar o 1 fazendo (1-x)>0, mas o menos nove não, ate achei mas não tenho certeza se a matematica que eu usei esta certa, se alguem puder ajudar com essa parte eu agradeço.
-
barizom
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Mar 27, 2010 13:39
- Formação Escolar: SUPLETIVO
- Área/Curso: Fisica
- Andamento: cursando
 por Molina » Sáb Mar 27, 2010 17:52
por Molina » Sáb Mar 27, 2010 17:52
barizom escreveu:O enunciado pede para encontrar o dominio da função.

A respota é: D(f)= x pertence aos reais tal que -9 maior ou igual a X e menor que 1.
Consegui achar o 1 fazendo (1-x)>0, mas o menos nove não, ate achei mas não tenho certeza se a matematica que eu usei esta certa, se alguem puder ajudar com essa parte eu agradeço.
Boa tarde, barizom.
Você terá que considerar as duas condições para essa função existir.
Lembramos que:
Com isso,
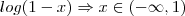 (intervalo 1)
(intervalo 1)E temos que
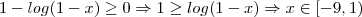 (intervalo 2)
(intervalo 2)Fazendo a intersecção dos intervalos 1 e 2, temos que
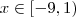

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por barizom » Sáb Mar 27, 2010 20:48
por barizom » Sáb Mar 27, 2010 20:48
No caso eu tinha feito desse jeito, mas achei estranho ignorar a raiz e o f(x).
Foi essa logica que eu não vi, como eu podia ignorar a raiz e o f(x) para achar o dominio, na verdade ainda não vi.
Tambem nao entendi o porque do maior ou igual n intervalo 2.
-
barizom
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sáb Mar 27, 2010 13:39
- Formação Escolar: SUPLETIVO
- Área/Curso: Fisica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Encontrar velocidade usando a Integral
por renanrdaros » Dom Abr 17, 2011 04:03
- 8 Respostas
- 4929 Exibições
- Última mensagem por renanrdaros

Seg Abr 18, 2011 11:35
Cálculo: Limites, Derivadas e Integrais
-
- [Encontrar Domínio]
por JessicaAraujo » Ter Abr 16, 2013 22:00
- 1 Respostas
- 827 Exibições
- Última mensagem por young_jedi

Qua Abr 17, 2013 11:47
Funções
-
- [Encontrar domínio e imagem]
por Larry Crowne » Sex Mar 29, 2013 21:46
- 1 Respostas
- 959 Exibições
- Última mensagem por nakagumahissao

Sáb Mar 30, 2013 01:48
Funções
-
- [Encontrar Domínio] Equação trigonométrica
por JessicaAraujo » Dom Abr 14, 2013 19:05
- 1 Respostas
- 947 Exibições
- Última mensagem por e8group

Dom Abr 14, 2013 19:32
Funções
-
- Logarítimo
por Adilson » Ter Ago 25, 2009 15:26
- 3 Respostas
- 2952 Exibições
- Última mensagem por Adilson

Qui Ago 27, 2009 13:27
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




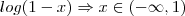
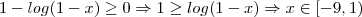
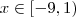



 .
.
 :
: