 por brumadense » Sex Mar 19, 2010 03:16
por brumadense » Sex Mar 19, 2010 03:16
Olá colegas
Gostaria de uma explicação de como essa função foi resolvida. Estou sentindo dificuldade em resolver funções quando aparecem com radicais. Alguém poderia me explicar como resolver quando aparece radicais, como no caso abaixo? Desde já agradeço.
Seja a função
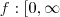
)

R dado por f
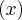
=
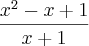
. Calcule:
![f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2} f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2}](/latexrender/pictures/02315716053abca173ab996ed26fafef.png)
-
brumadense
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Jan 15, 2010 00:06
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Sex Mar 19, 2010 09:17
por Molina » Sex Mar 19, 2010 09:17
brumadense escreveu:Olá colegas
Gostaria de uma explicação de como essa função foi resolvida. Estou sentindo dificuldade em resolver funções quando aparecem com radicais. Alguém poderia me explicar como resolver quando aparece radicais, como no caso abaixo? Desde já agradeço.
Seja a função
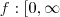
)

R dado por f
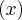
=
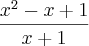
. Calcule:
![f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2} f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2}](/latexrender/pictures/02315716053abca173ab996ed26fafef.png)
Bom dia.
Dada esta função
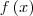
=
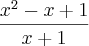
queremos encontrar
![f \left(\sqrt[2]{2}-1 \right) f \left(\sqrt[2]{2}-1 \right)](/latexrender/pictures/90d35ea6766006e5e36ab952c432473a.png)
, ou seja, vamos substituir todos os x da equação por
![\sqrt[2]{2}-1 \sqrt[2]{2}-1](/latexrender/pictures/f04f8b4ee7780eec1f1bd142c7b476fd.png)
. E foi isso que foi feito.
Os procedimentos seguintes foi só algebrismo. Elevar ao quadrado, somar, subtrair, etc. Porém, o denominador da fração (parte de baixo) ficou com raiz. Quando isso acontece temos que racionalizar esta fração, ou seja, eliminar essa raiz de baixo. Para fazer isso o truque é sempre o mesmo: multiplicar pela própria raiz. Só que temos que multiplicar em cima e embaixo. E foi isso que foi feito, multiplicando por

.
Qualquer dúvida, avise!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Preciso de uma explicação
por Deko » Dom Mar 28, 2010 16:33
- 1 Respostas
- 1710 Exibições
- Última mensagem por Elcioschin

Dom Mar 28, 2010 19:07
Cálculo: Limites, Derivadas e Integrais
-
- explicação calculo
por crsglc2 » Dom Abr 04, 2010 23:21
- 1 Respostas
- 2662 Exibições
- Última mensagem por Molina

Ter Abr 06, 2010 21:58
Cálculo: Limites, Derivadas e Integrais
-
- Preciso de Explicação
por andersonvendramin28 » Ter Mai 31, 2011 11:29
- 8 Respostas
- 8318 Exibições
- Última mensagem por andersonvendramin28

Qua Jun 08, 2011 15:46
Funções
-
- Explicação da tangente
por Cleyson007 » Qua Out 17, 2012 16:48
- 3 Respostas
- 3881 Exibições
- Última mensagem por Cleyson007

Qui Out 18, 2012 09:14
Trigonometria
-
- DUVIDA- EXPLICAÇÃO
por zenildo » Qui Dez 19, 2013 12:01
- 0 Respostas
- 1070 Exibições
- Última mensagem por zenildo

Qui Dez 19, 2013 12:01
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
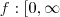 )
) R dado por f
R dado por f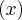 =
=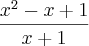 . Calcule:
. Calcule:![f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2} f \left(\sqrt[2]{2}-1 \right)=\frac{{\left(\sqrt[2]{2}-1 \right)}^{2}-\left(\sqrt[2]{2}-1 \right)+1}{\sqrt[2]{2}-1+1}=\frac{2-2\sqrt[2]{2}+1-\sqrt[2]{2}+1+1}{\sqrt[2]{2}}=\frac{5-3\sqrt[2]{2}}{\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-3\sqrt[2]{2}.\sqrt[2]{2}}{\sqrt[2]{2}.\sqrt[2]{2}}=\frac{5\sqrt[2]{2}-6}{2}](/latexrender/pictures/02315716053abca173ab996ed26fafef.png)


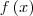 =
=![f \left(\sqrt[2]{2}-1 \right) f \left(\sqrt[2]{2}-1 \right)](/latexrender/pictures/90d35ea6766006e5e36ab952c432473a.png) , ou seja, vamos substituir todos os x da equação por
, ou seja, vamos substituir todos os x da equação por ![\sqrt[2]{2}-1 \sqrt[2]{2}-1](/latexrender/pictures/f04f8b4ee7780eec1f1bd142c7b476fd.png) . E foi isso que foi feito.
. E foi isso que foi feito. .
.
