(MACKENZIE) Se f(x) = mx + n e f(f(x)) = 4x + 9, a soma dos possíveis valores de n é:
Tenho dificuldade nas operações do exercício.



Douglaspimentel escreveu:(MACKENZIE) Se f(x) = mx + n e f(f(x)) = 4x + 9, a soma dos possíveis valores de n é:
Tenho dificuldade nas operações do exercício.



![f(f(x))=m[f(x)]+n f(f(x))=m[f(x)]+n](/latexrender/pictures/e8d597d7d99f4fa90dcdeb77481644b5.png)
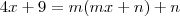
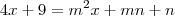

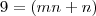
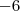 .
. 

![\sqrt[2]{x+1} \sqrt[2]{x+1}](/latexrender/pictures/1a4918c18d7e32bcc010b0b56b47de5f.png) , g(x) =
, g(x) = 
 ) , D(g) = R*
) , D(g) = R* ) , Im(g) = R*
) , Im(g) = R* ), só que ae daria uma raiz de número negativo, e a minha área de estudo são só os número reais. Então acho que a minha resposta esteja certa. Se estiver errada, por favor corrijam, e as outras também.
), só que ae daria uma raiz de número negativo, e a minha área de estudo são só os número reais. Então acho que a minha resposta esteja certa. Se estiver errada, por favor corrijam, e as outras também. 
![\sqrt[2]{\frac{1}{x}+1} \sqrt[2]{\frac{1}{x}+1}](/latexrender/pictures/6f1994aa5204c6a5802fb993b0dee59f.png) , o domínio de f(g(x)) consiste nos números x do domínio de g para os quais g(x) estejam no domínio de f, certo? Existe uma definição mais simples? Uma forma mais simples de achar o domínio da função composta? Ou alguém poderia me explicar isso mais claramente?
, o domínio de f(g(x)) consiste nos números x do domínio de g para os quais g(x) estejam no domínio de f, certo? Existe uma definição mais simples? Uma forma mais simples de achar o domínio da função composta? Ou alguém poderia me explicar isso mais claramente? 
![\frac{1}{\sqrt[2]{x+1}} \frac{1}{\sqrt[2]{x+1}}](/latexrender/pictures/ec85e04a67f07d73544a1e5397d16e4e.png)




Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante