por Vencill » Qua Dez 03, 2014 17:42
Olá Boa tarde!
Estou com dúvidas no seguinte exercício:
Determinar os números críticos da seguinte função
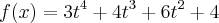
Agradeço pela ajuda é que estou aprendendo agora números críticos e estou com dúvidas.
-
Vencill
- Usuário Ativo
-
- Mensagens: 10
- Registrado em: Qui Nov 13, 2014 16:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
por Cleyson007 » Qua Dez 03, 2014 18:12
Olá, boa tarde!
Basta derivar a função f(x) e igualar a zero.
f' (t) = 12t³ + 12t² +12t
Coloca o 12t em evidência e iguala a zero.
Qualquer dúvida estou em disposição.
Abraço
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
por Vencill » Qua Dez 03, 2014 23:10
colocando o 12t em evidencia o resultado seria: 3+4+1=0?
Esta correto?
-
Vencill
- Usuário Ativo
-
- Mensagens: 10
- Registrado em: Qui Nov 13, 2014 16:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
por Cleyson007 » Qui Dez 04, 2014 08:21
Olá, bom dia!
Não..
Colocando o 12t em evidência, temos:
12t(t² + t + 1)
Logo, 12t = 0 --> t = 0
Ou t² + t + 1 = 0 (Essa equação do segundo não possui raízes reais). Lembra que o(s) número(s) crítico(s) deve(m) pertencer ao domínio da f(x)?
Pois é, o domínio da nossa f(x) é o conjunto dos números reais. Logo, somente 0 é número crítico.
Abraço
-
Cleyson007
- Colaborador Voluntário
-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Numeros criticos!!!
por aline_n » Qua Jun 01, 2011 18:59
- 1 Respostas
- 1290 Exibições
- Última mensagem por carlosalesouza
Qua Jun 01, 2011 19:19
Cálculo: Limites, Derivadas e Integrais
-
- Numeros criticos
por aline_n » Qua Jun 01, 2011 20:14
- 5 Respostas
- 3926 Exibições
- Última mensagem por carlosalesouza
Qui Jun 02, 2011 18:33
Cálculo: Limites, Derivadas e Integrais
-
- Números Críticos
por Cleyson007 » Ter Jan 28, 2014 18:42
- 5 Respostas
- 2621 Exibições
- Última mensagem por Cleyson007
Qua Jan 29, 2014 08:11
Cálculo: Limites, Derivadas e Integrais
-
- Números Críticos
por Carolwis » Sáb Nov 15, 2014 14:39
- 1 Respostas
- 1424 Exibições
- Última mensagem por adauto martins
Qua Nov 19, 2014 14:36
Cálculo: Limites, Derivadas e Integrais
-
- Números críticos da função
por Vencill » Ter Dez 02, 2014 17:38
- 1 Respostas
- 1158 Exibições
- Última mensagem por Cleyson007
Ter Dez 02, 2014 18:04
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
