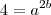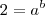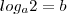por Maira » Sáb Dez 19, 2009 16:47
por Maira » Sáb Dez 19, 2009 16:47
Alguém poderia me ajudar na questão de funções da UFJF 2009?
É a questão 11 desta prova:
http://siga.ufjf.br/index.php?module=ve ... va1a_2.pdfAguardo respostas, obrigada!
-
Maira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 19, 2009 16:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Sáb Dez 19, 2009 18:45
por MarceloFantini » Sáb Dez 19, 2009 18:45
Como os pontos

e

são obtidos a partir da intersecção do gráfico

com
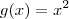
, vamos obter as ordenadas substituindo em

.
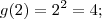
e

. Logo, tem-se:

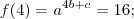
Aplicando logaritmo na base

dos dois lados (uma vez que

e
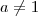
pelo enunciado), temos:


Resolvendo-se o sistema, encontramos que

. Logo:
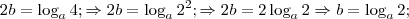
Ou, como está na alternativa
E:

.
Acredito ser essa a resposta.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Sáb Dez 19, 2009 19:06
por Molina » Sáb Dez 19, 2009 19:06
Boa tarde, Maira.
Vamos ver se posso ajudar.
O dado mais importante que ele nos fornece é onde esses pontos P e Q estão na abscissa (2 e 4).
Ou seja, sabemos que em

e

os gráficos se cruzam.
Temos então que

e

. Mas
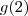
e
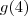
é fácil de achar:


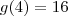
Com isso, temos que
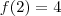
e
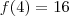
. Vamos usar este resultado agora:
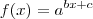
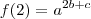
 (equação 1)
(equação 1)
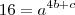 (equação 2)
(equação 2)Dividindo a equação 2 pela equação 1, obtemos:
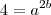

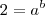
E isso nos dá o seguinte logaritmo:
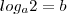
Por isso eu assinalaria a alternativa e).

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Maira » Sáb Dez 19, 2009 19:27
por Maira » Sáb Dez 19, 2009 19:27
Obrigada professores, estou numa maratona da ufjf aqui,
muito obrigada
-
Maira
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Dez 19, 2009 16:40
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão UFJF
por Guilherme Carvalho » Sex Mai 13, 2011 12:19
- 1 Respostas
- 1485 Exibições
- Última mensagem por MarceloFantini

Sex Mai 13, 2011 15:54
Trigonometria
-
- Questão UFJF
por Guilherme Carvalho » Ter Mai 31, 2011 15:42
- 1 Respostas
- 2052 Exibições
- Última mensagem por Claudin

Ter Mai 31, 2011 18:04
Funções
-
- [Função Exponencial] UFJF - MG
por SCHOOLGIRL+T » Sáb Nov 10, 2012 17:52
- 4 Respostas
- 2155 Exibições
- Última mensagem por e8group

Sáb Nov 10, 2012 18:46
Álgebra Elementar
-
- questão função
por sheila » Qui Set 06, 2007 22:37
- 4 Respostas
- 7818 Exibições
- Última mensagem por admin

Ter Set 11, 2007 16:39
Funções
-
- Questão de Funçao
por kael » Qui Mar 05, 2009 16:30
- 4 Respostas
- 2971 Exibições
- Última mensagem por Molina

Sex Mar 06, 2009 12:47
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e  são obtidos a partir da intersecção do gráfico
são obtidos a partir da intersecção do gráfico  com
com 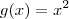 , vamos obter as ordenadas substituindo em
, vamos obter as ordenadas substituindo em  .
. 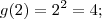 e
e  . Logo, tem-se:
. Logo, tem-se:
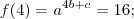
 dos dois lados (uma vez que
dos dois lados (uma vez que  e
e 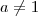 pelo enunciado), temos:
pelo enunciado), temos:

 . Logo:
. Logo: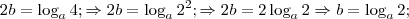
 .
.

 e
e  os gráficos se cruzam.
os gráficos se cruzam. e
e  . Mas
. Mas 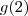 e
e 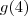 é fácil de achar:
é fácil de achar:

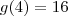
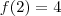 e
e 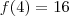 . Vamos usar este resultado agora:
. Vamos usar este resultado agora: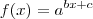
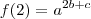
 (equação 1)
(equação 1)
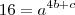 (equação 2)
(equação 2)