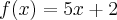 e
e  . Determine a lei que define a função afim h, sabendo que
. Determine a lei que define a função afim h, sabendo que 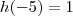 e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.
e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.Não consegui nem iniciar a resolução =/

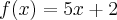 e
e  . Determine a lei que define a função afim h, sabendo que
. Determine a lei que define a função afim h, sabendo que 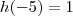 e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.
e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.








Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.



