Bom, estou com algumas dúvidas sobre inequação modular. Me deparei com alguns problemas que eu não consegui resolver e outros que a minha resposta não "batia" com o gabarito.
Vou mostra-las:
1-
 ;
;2-
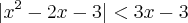 ;
;Essas duas últimas, por favor, sejam mais didáticos!
3-
 ;
;4-
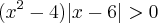 ;
;Nas duas ultimas tive dificuldade me saber como fazer os sinais, por exemplo na 4 eu resolvi assim:
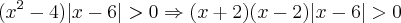
A partir dai eu fiz as duas possível equações, com o modulo positivo e igual a zero e com o modulo negativo.

na minha visão funcionaria como duas equações de segundo grau tendo raizes 2,-2,6 (ambas) Porem agora fica o problema. Vou fazer a reta com a primeira equação e outra com a segunda.
______-____+_____-____+
 ___-2____2____6____
___-2____2____6____ onde o conjunto solução da primeira seria
onde o conjunto solução da primeira seria ![S=]-2,2[\cup]6,+\infty[ S=]-2,2[\cup]6,+\infty[](/latexrender/pictures/db893c15447fc9fe16a6067424029f77.png) testamos e veremos que apenas os > que 6 funcionam na equação e assim
testamos e veremos que apenas os > que 6 funcionam na equação e assim ![S=]6,+\infty[ S=]6,+\infty[](/latexrender/pictures/707cdc4581488670db73fa440ead62c6.png)
![S=]6,+\infty[ S=]6,+\infty[](/latexrender/pictures/707cdc4581488670db73fa440ead62c6.png)
e a segunda ficaria assim:
______+____-_____+____-
 ___-2____2____6____
___-2____2____6____ onde o conjunto solução seria
onde o conjunto solução seria ![S=]-\infty,-2[\cup]2,6[ S=]-\infty,-2[\cup]2,6[](/latexrender/pictures/f4b85739a91b998a8c8aad1e0e41eb45.png) testamos e veremos que apenas os
testamos e veremos que apenas os ![S=]2,6[ S=]2,6[](/latexrender/pictures/c1cf08bae416e925fefe7efb5ec81e1c.png) funcionam.
funcionam.Então como resposta final ficaria
![S=]2,+\infty[ S=]2,+\infty[](/latexrender/pictures/c136133593766ec66533177003fcfb81.png) , Estou errado????
, Estou errado????Por favor! Me ajudem


 .Onde ,
.Onde , são funções e
são funções e  uma cosntante . Temos então 4 casos a considerar :
uma cosntante . Temos então 4 casos a considerar : 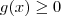 e
e  .
. e
e 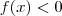
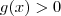 e
e 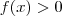
 são conjuntos de números tais que :
são conjuntos de números tais que : 
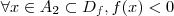
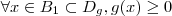


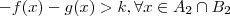

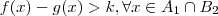 .
.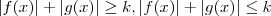 (neste caso obrigatoriamente
(neste caso obrigatoriamente  ) ,
) ,  .
. ou
ou  em que
em que  ,
, 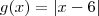 e
e  ???
??? 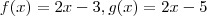 e
e  ,qual a solução da desigualdade
,qual a solução da desigualdade  ????
???? e
e  pois
pois  .
. 