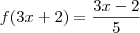 e
e 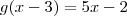 ,então
,então 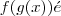 :
:a-)x-4/4
b-)5x-9/5
c-)5x+13
d-)5x+11/5

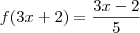 e
e 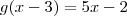 ,então
,então 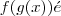 :
:

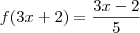 , a estratégia agora é fazer aparecer o 3x+2.somando e subtraindo 2 da parte de cima da fração.
, a estratégia agora é fazer aparecer o 3x+2.somando e subtraindo 2 da parte de cima da fração.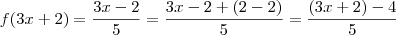 .Perceba que posso chamar (3x+2) de x ,imagine que ele tivesse uma função f(x) e trocasse de variavel para um f(y) por exemplo mas "y" pode ser também uma função nesse caso uma função igual a (3x+2),usando a mesma técnica em g(x).
.Perceba que posso chamar (3x+2) de x ,imagine que ele tivesse uma função f(x) e trocasse de variavel para um f(y) por exemplo mas "y" pode ser também uma função nesse caso uma função igual a (3x+2),usando a mesma técnica em g(x).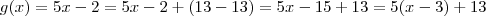 .Posso agora chamar (x-3) de x.Ficando com:
.Posso agora chamar (x-3) de x.Ficando com: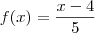 e
e 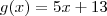 .Utilizando a função composto que é basicamente trocar a variavel de f pela função g.
.Utilizando a função composto que é basicamente trocar a variavel de f pela função g.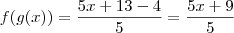

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

