O enunciado diz que o gráfico mostra uma função
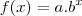 e o gráfico representa a inflação de um país . Ele pede a taxa de inflação no quarto ano (f(4)).
e o gráfico representa a inflação de um país . Ele pede a taxa de inflação no quarto ano (f(4)).
O gráfico está ruim pois foi feito no PAINT. Só para constar, a "reta" corta o eixo Y no 960.
Aí vem minha principal dúvida:
Temos os pontos (0,960). Então
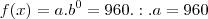
Substituindo em outros pontos ( 7 , 7,5 ), eu encontro um resultado absurdo.
PS: A resposta é 30%.
Onde está meu erro? Qual é a maneira correta de se fazer?
Obrigado



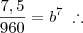
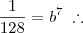

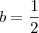
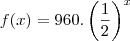


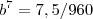 pois achei complicado calcular a raíz sétima de 7,5/960. Bom , é possível que haja mesmo erro de gabarito. Quinta Feira terei aula de álgebra e pedirei ao professor que resolva tal questão. Veremos se tem tal erro. Obrigado.
pois achei complicado calcular a raíz sétima de 7,5/960. Bom , é possível que haja mesmo erro de gabarito. Quinta Feira terei aula de álgebra e pedirei ao professor que resolva tal questão. Veremos se tem tal erro. Obrigado.

 , avisa que eu resolvo.
, avisa que eu resolvo.

