 por Carolziiinhaaah » Qui Ago 12, 2010 11:34
por Carolziiinhaaah » Qui Ago 12, 2010 11:34
Um avião tem combustível para voar durante 4 horas. Na presença de um vento com velocidade v km/h na direção e sentido do movimento, a velocidade do avião é de (300 + v) km/h. Se o avião se desloca em sentido contrário ao do vento, sua velocidade é de (300 - v) km/h. Suponha que o avião se afaste a uma distância d do aeroporto e retorne ao ponto de partida, consumindo todo o combustível, e que durante todo o trajeto a velocidade do vento é constante e tem a mesma direção que a do movimento do avião.
a) Determine d como função de v.
b) Determine para que valor de v a distância d é
máxima.
gabaritos:
a)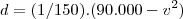 b)
b) 
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Qui Ago 12, 2010 13:14
por Douglasm » Qui Ago 12, 2010 13:14
Bom, primeiramente, temos que considerar o tempo que leva-se na ida (em que considerarei que o vento está a favor) e o tempo que se leva na volta (quando o vento está contra o movimento do avião). Depois disso, basta somarmos os tempos (pois já temos o tempo total de 4 hrs) e teremos
d em função de
v. Comecemos:
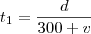

Somando-os:
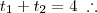

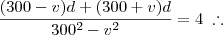
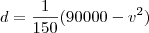
Sobre a letra b, o que se pede é a distância máxima que o avião percorerá, não o valor de
v nesse caso. Só de observar a função acima, vemos que
d é máximo para
v = 0 e que é igual a 600km.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função] Questão UFRJ.
por replay » Qua Out 10, 2012 21:37
- 12 Respostas
- 12156 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 21:29
Funções
-
- (UFRJ 2009 ) Questão do vestibular da ufrj em 2009 me ajudem
por rafael84 » Ter Jul 13, 2010 22:57
- 1 Respostas
- 2586 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 15, 2010 01:28
Binômio de Newton
-
- Questão da Ufrj
por 321 » Ter Ago 31, 2010 02:32
- 0 Respostas
- 2871 Exibições
- Última mensagem por 321

Ter Ago 31, 2010 02:32
Matrizes e Determinantes
-
- Questão concurso UFRJ
por sun123+ » Qui Dez 11, 2014 19:22
- 1 Respostas
- 1500 Exibições
- Última mensagem por nakagumahissao

Sex Dez 12, 2014 19:42
Equações
-
- (UFRJ) Função
por aline2010 » Qui Jun 17, 2010 20:43
- 1 Respostas
- 1293 Exibições
- Última mensagem por Tom

Sex Jul 02, 2010 20:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
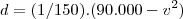


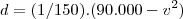


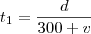

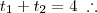

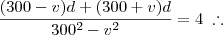
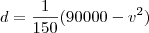



 , avisa que eu resolvo.
, avisa que eu resolvo.

