 ,definida por:
,definida por: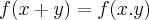 ...mostre que:
...mostre que:a) f nao admite funçao inversa.
b)x,y sao necessariamente numeros irracionais.
soluçao:
a)
seja
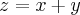 ,logo:
,logo: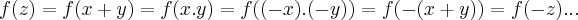
portanto f é uma funçao par,e nao é injetiva(mostre isso),logo nao admite funçao inversa.
b)
seja
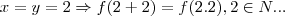
seja
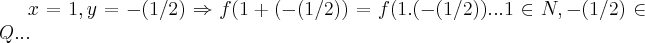

 ,definida por:
,definida por: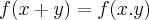 ...mostre que:
...mostre que: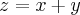 ,logo:
,logo: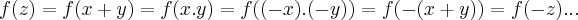
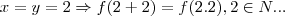
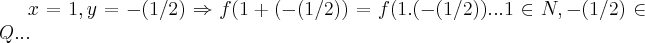

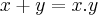 ,pois teriamos q. ter:
,pois teriamos q. ter: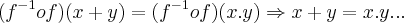 ...
...
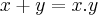 ,pois invalidaremos a condiçao de nao existencia da funçao inversa.
,pois invalidaremos a condiçao de nao existencia da funçao inversa.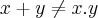 .entao busquemos um
.entao busquemos um 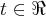 ,
,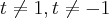 (pq
(pq 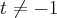 ?),tal que
?),tal que 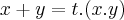 ...logo:
...logo: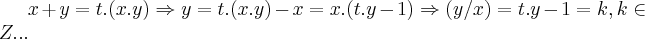 .
.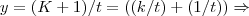 ,para q.
,para q. 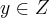 ,teriamos q. ter
,teriamos q. ter  ,ao qual invalidaria a nossa condiçao de nao existencia da inversa...logo, y nao pode ser inteiro...
,ao qual invalidaria a nossa condiçao de nao existencia da inversa...logo, y nao pode ser inteiro...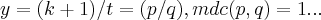
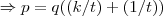
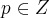 ,t teria q. ser igual a um,o q. como visto anteriormente contradiz a condiçao de nao inversa...logo y nao pode ser racional...modo analogo para x...entao x,y teem q. ser irracionais...
,t teria q. ser igual a um,o q. como visto anteriormente contradiz a condiçao de nao inversa...logo y nao pode ser racional...modo analogo para x...entao x,y teem q. ser irracionais...
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

