 por guijermous » Qui Fev 25, 2010 17:33
por guijermous » Qui Fev 25, 2010 17:33
Comecei estudar funções exponencias, e pensei que ia ser fácil, mas me equivoquei. rs
Não consegui fazer uns exercícios que parecem ser bem básicos, poderiam me ajudar?
1) Uma das raízes da equação
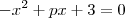
é igual a 2. Determine p.
2)(FEI-SP) Uma das raízes da equação

é também raiz da equação
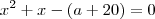
. Qual valor de a?
3) Diferença entre as raízes da equação

é igual a 1/2. Calcule valor de M.
4) As raízes da equação
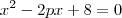
são positivas, e uma é o dobro da outra. Qual valor de p?
Eu tenho meio que dificuldade sempre nessas questões que colocam incógnitas no meio. Não consegui solucionar nenhuma delas, e não parece ser um bicho de sete cabeças =/
E tem essa aqui que estou indignado. rsrs
(UFMG)
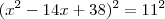
. Qntas raizes reais distintas possui?
Não são duas?

Desculpem o numero de questões acima, mas eu achei mais fácil colocá-las juntas e alguém me ajudar, mesmo que seja uma ou outra do que criar vários tópicos. rs
Obrigado!
-
guijermous
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Fev 15, 2010 14:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Inf. Industrial
- Andamento: formado
 por Molina » Qui Fev 25, 2010 17:42
por Molina » Qui Fev 25, 2010 17:42
Boa tarde.
guijermous escreveu:1) Uma das raízes da equação
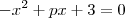
é igual a 2. Determine p.
Podemos usar o princípio da
soma e produto pra resolver questões deste tipo.
Então temos o seguinte:
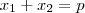
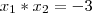
Só que
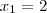
(pelo enunciado)...
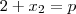
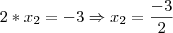
Sobstituindo

em
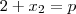
temos que
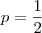
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Qui Fev 25, 2010 17:46
por Molina » Qui Fev 25, 2010 17:46
Só duas observações...
Da 2) a 4) você consegue resolver pelo mesmo método apresentado na questão 1)
Essas suas questões não se trata de função e nem de exponencial. São Equações de 2° grau. Exponencial é no caso da variável ser um expoente, por exemplo:  . Por este motivo vou estar corrigindo o título de seu tópico.
. Por este motivo vou estar corrigindo o título de seu tópico.
Abraços! 
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por guijermous » Qui Fev 25, 2010 21:18
por guijermous » Qui Fev 25, 2010 21:18
Obrigado!
Consegui fazer todas menos a segunda, da FEI-SP, poderia me ajudar?
E a da UFMG ? Poderia me explicar porque 3 raízes?
-
guijermous
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Fev 15, 2010 14:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Inf. Industrial
- Andamento: formado
 por Molina » Qui Fev 25, 2010 22:19
por Molina » Qui Fev 25, 2010 22:19
guijermous escreveu:2)(FEI-SP) Uma das raízes da equação

é também raiz da equação
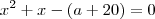
. Qual valor de a?
Confesso que essa não consegui. Tomara que alguém te ajude...
Quanto a questão a UFMG você pode tirar a raiz quadrada de ambos os lados:
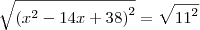
O resultado é dado em módulo:

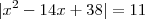
Usando a propriedade de módulo você terá que resolver essas duas equações:
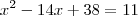

E verá que esta segunda admite duas raízes iguais (7).
Por isso a resposta é 3 raízes.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por guijermous » Sex Fev 26, 2010 12:02
por guijermous » Sex Fev 26, 2010 12:02
ahh sim. entendi
xD
obrigado!
bem, ainda estou com umas dúvidas e irei continuar nesse topico. rs
Se tenho duas raízes, e quero achar a função da equação, eu faço
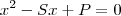
, onde S = soma e P = produto.
Mas agora estou com um exercício que não consegui determinar a função.. o exercício pede a f(x) do gráfico apresentado.
O gráfico é uma equação de segundo grau, com a concavidade virada para cima (positivo), tendo apenas uma raíz real,

, e cortando o eixo Y no ponto 3. Só.. não consegui determinar f(x), alguem poderia me ajudar?
Outra, tenho duas equações: da reta,
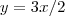
que eu achei de uma reta A (e está correto), e que foi dado de uma função B
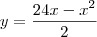
.
O exercício letra B) peede para dizer quando A e B atingiram a mesma altura, e qual foi..
Só que não consegui determinar quando as duas se batem, igualei elas mas nada... elas estão em função x(dias) por y(altura)..
Se alguem poder me ajudar, ou sugerir algo, agradeço. obrigado!!

-
guijermous
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Fev 15, 2010 14:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Inf. Industrial
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do 1º Grau - Como montar a equação
por macedo1967 » Sáb Out 07, 2017 12:53
- 1 Respostas
- 8032 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:17
Equações
-
- [Equação Modular] com equação de 2º grau
por paola-carneiro » Qui Abr 05, 2012 15:53
- 2 Respostas
- 3410 Exibições
- Última mensagem por paola-carneiro

Sex Abr 06, 2012 16:23
Funções
-
- Equação do 1 Grau
por luanxd » Ter Jan 26, 2010 00:06
- 3 Respostas
- 5505 Exibições
- Última mensagem por Cleyson007

Qua Jan 27, 2010 20:40
Polinômios
-
- equação do 2º grau
por juniorthai » Seg Fev 08, 2010 12:05
- 2 Respostas
- 11747 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 06, 2010 20:48
Trigonometria
-
- equação do 2º grau
por juniorthai » Qui Fev 11, 2010 08:15
- 6 Respostas
- 8336 Exibições
- Última mensagem por lulopes

Sex Dez 08, 2017 20:05
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
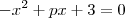 é igual a 2. Determine p.
é igual a 2. Determine p. é também raiz da equação
é também raiz da equação 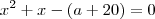 . Qual valor de a?
. Qual valor de a? é igual a 1/2. Calcule valor de M.
é igual a 1/2. Calcule valor de M.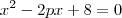 são positivas, e uma é o dobro da outra. Qual valor de p?
são positivas, e uma é o dobro da outra. Qual valor de p?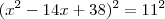 . Qntas raizes reais distintas possui?
. Qntas raizes reais distintas possui?


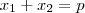
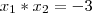
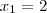 (pelo enunciado)...
(pelo enunciado)...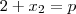
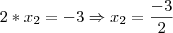
 em
em 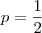

 .
. 
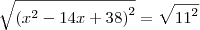

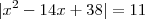
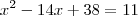

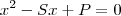 , onde S = soma e P = produto.
, onde S = soma e P = produto. , e cortando o eixo Y no ponto 3. Só.. não consegui determinar f(x), alguem poderia me ajudar?
, e cortando o eixo Y no ponto 3. Só.. não consegui determinar f(x), alguem poderia me ajudar?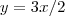 que eu achei de uma reta A (e está correto), e que foi dado de uma função B
que eu achei de uma reta A (e está correto), e que foi dado de uma função B 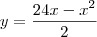 .
.




