Não consegui fazer uns exercícios que parecem ser bem básicos, poderiam me ajudar?
1) Uma das raízes da equação
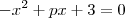 é igual a 2. Determine p.
é igual a 2. Determine p.2)(FEI-SP) Uma das raízes da equação
 é também raiz da equação
é também raiz da equação 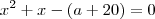 . Qual valor de a?
. Qual valor de a?3) Diferença entre as raízes da equação
 é igual a 1/2. Calcule valor de M.
é igual a 1/2. Calcule valor de M.4) As raízes da equação
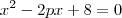 são positivas, e uma é o dobro da outra. Qual valor de p?
são positivas, e uma é o dobro da outra. Qual valor de p?Eu tenho meio que dificuldade sempre nessas questões que colocam incógnitas no meio. Não consegui solucionar nenhuma delas, e não parece ser um bicho de sete cabeças =/
E tem essa aqui que estou indignado. rsrs
(UFMG)
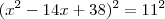 . Qntas raizes reais distintas possui?
. Qntas raizes reais distintas possui?Não são duas?

Desculpem o numero de questões acima, mas eu achei mais fácil colocá-las juntas e alguém me ajudar, mesmo que seja uma ou outra do que criar vários tópicos. rs
Obrigado!


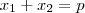
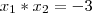
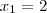 (pelo enunciado)...
(pelo enunciado)...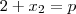
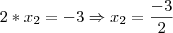
 em
em 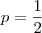

 .
. 
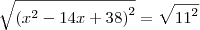

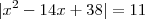
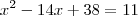

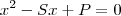 , onde S = soma e P = produto.
, onde S = soma e P = produto. , e cortando o eixo Y no ponto 3. Só.. não consegui determinar f(x), alguem poderia me ajudar?
, e cortando o eixo Y no ponto 3. Só.. não consegui determinar f(x), alguem poderia me ajudar?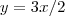 que eu achei de uma reta A (e está correto), e que foi dado de uma função B
que eu achei de uma reta A (e está correto), e que foi dado de uma função B 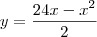 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)