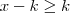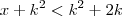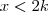por guijermous » Seg Fev 22, 2010 17:36
por guijermous » Seg Fev 22, 2010 17:36
Galera, estou tentando encerrar meu estudo na função afim, e há alguns exercícios que não consegui fazer de jeito nenhum !
Vou colocá-los aqui, e quem souber e me ajudar vou ser muito grato !
(Fuvest-SP) Qual é o conjunto solução da inequeação
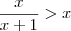
?
Agora, tem esse aqui. Eu sei que é fácil, tem uns 3 desse tipo, mas se eu conseguir resolver um consigo os demais.
(UFF-RJ) As empresas Alfa e Beta alugam televisores do mesmo tipo. A empresa Alfa cobra R$ 35,00 fixos pelos 30 primeiros dias de uso e R$ 1,00 por dia extra. A empresa Beta cobra R$ 15,00 pelos primeiros 20 dias de uso e R$ 1,50 por dia extra. Após N dias, o valor cobrado pela empresa Beta passa a ser maior que o do cobrado pela empresa Alfa. O valor de N é?
E este aqui meio chato.
(PUC-RJ) Seja K um número positivo. Então o conjunto dos números X tais que
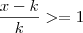
e
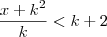
é?
Esse negócio de usar K no meio de inequações, não tenho idéia do que fazer!
Quem souber algum desses me ajuda ae por favor !
Muito obrigado!

Abrs
-
guijermous
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Seg Fev 15, 2010 14:38
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Inf. Industrial
- Andamento: formado
 por MarceloFantini » Seg Fev 22, 2010 20:54
por MarceloFantini » Seg Fev 22, 2010 20:54
Boa noite!
(FUVEST)
Primeiro, lembre-se de que
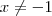
. Agora, multiplicando-se os dois lados por

:
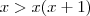
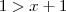
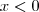
Portanto:
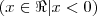
(UFF-RJ)
Empresa Alfa:
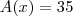
para
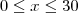
;
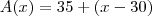
para
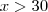
Empresa Beta:
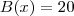
para
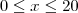

para
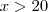
Se você plotar o gráfico, verá que em

, o custo é o mesmo. Em
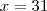
, o custo passa. Algebricamente:

para
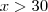
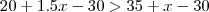
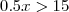
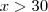
(PUC-RJ)
Como

, multiplicando as duas desigualdades por

temos:
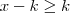
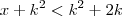
Logo:

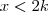
Portanto, acredito que seja conjunto vazio.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercícios que não consegui fazer! Me ajudem?!
por mtuliopaula » Seg Nov 09, 2009 14:46
- 1 Respostas
- 6359 Exibições
- Última mensagem por Neperiano

Dom Set 18, 2011 13:50
Estatística
-
- [Função afim] Determinar a função afim
por Apprentice » Dom Set 30, 2012 21:49
- 4 Respostas
- 3237 Exibições
- Última mensagem por Apprentice

Seg Out 01, 2012 12:19
Funções
-
- funçao afim
por maiara amaral » Dom Mai 11, 2008 18:08
- 2 Respostas
- 4875 Exibições
- Última mensagem por Kabarosk

Sex Mai 29, 2015 01:45
Pedidos
-
- Funçao Afim
por thais silva » Qua Mai 19, 2010 17:30
- 3 Respostas
- 2990 Exibições
- Última mensagem por MarceloFantini

Seg Jul 12, 2010 22:04
Funções
-
- funçao afim
por emilly » Ter Ago 17, 2010 20:40
- 6 Respostas
- 7224 Exibições
- Última mensagem por emilly

Qui Ago 19, 2010 18:32
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
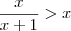 ?
?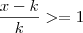 e
e 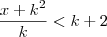 é?
é?


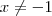 . Agora, multiplicando-se os dois lados por
. Agora, multiplicando-se os dois lados por  :
: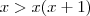
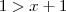
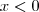
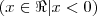
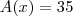 para
para 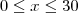 ;
;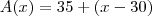 para
para 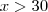
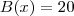 para
para 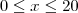
 para
para 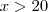
 , o custo é o mesmo. Em
, o custo é o mesmo. Em 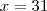 , o custo passa. Algebricamente:
, o custo passa. Algebricamente: para
para 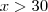
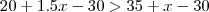
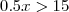
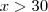
 , multiplicando as duas desigualdades por
, multiplicando as duas desigualdades por  temos:
temos: