
Dados os conjuntos A={x?R|1?x?3} B={x?R|-2?x?2} e C={x?R|-4?x?1} representar graficamente os seguintes produtos:
a) AxB
b)AxC
c)BxC



 ...eh o conjunto de todos os pares ordenadas (a,b)...aqui
...eh o conjunto de todos os pares ordenadas (a,b)...aqui 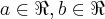 ,logo
,logo 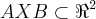 q. sera um quadrado no plano ,de lados 2 e 4...2=3-1,4=2-(-2)
q. sera um quadrado no plano ,de lados 2 e 4...2=3-1,4=2-(-2)

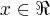 ,q.eh uma propriedade dada no problema...logo o conj. de todos pares ordenados AXB,eh um retangulo contido no plano...o grafico aqui nao eh uma curva,e sim uma area,eh como vc desenhasse um retangulo,no sistema cartesiano e o colorisse... como vc esta os colocando(num.inteiros) ai sim seriam pontos no plano cartesiano...vc deve prestar sempre atençao na propriedade dada no conjunto...um conj. generico eh assim definido...seja A={
,q.eh uma propriedade dada no problema...logo o conj. de todos pares ordenados AXB,eh um retangulo contido no plano...o grafico aqui nao eh uma curva,e sim uma area,eh como vc desenhasse um retangulo,no sistema cartesiano e o colorisse... como vc esta os colocando(num.inteiros) ai sim seriam pontos no plano cartesiano...vc deve prestar sempre atençao na propriedade dada no conjunto...um conj. generico eh assim definido...seja A={ conj./x tem propriedade tal}...exemplo...seja A={plantas/as plantas sao arvores frutiferas}...e por ai...
conj./x tem propriedade tal}...exemplo...seja A={plantas/as plantas sao arvores frutiferas}...e por ai...
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)