 por Miya » Seg Mar 30, 2015 10:21
por Miya » Seg Mar 30, 2015 10:21
NÃO CONSIGO ENTENDER por favor me ajudem!

Dados os conjuntos A={x?R|1?x?3} B={x?R|-2?x?2} e C={x?R|-4?x?1} representar graficamente os seguintes produtos:
a) AxB
b)AxC
c)BxC
-
Miya
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qui Mar 05, 2015 16:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Seg Mar 30, 2015 21:25
por adauto martins » Seg Mar 30, 2015 21:25
a)

...eh o conjunto de todos os pares ordenadas (a,b)...aqui
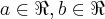
,logo
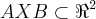
q. sera um quadrado no plano ,de lados 2 e 4...2=3-1,4=2-(-2)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Miya » Ter Mar 31, 2015 10:20
por Miya » Ter Mar 31, 2015 10:20
Então é certo fazer assim ?
se A={x?R|1?x?3} então o conjunto A são os números 1,2,3
se B={x?R|-2?x?2} então sãos os números -2,-1,0,1 e 2
e se C={x?R|-4< x?1} então -3,-2,-1,0 e 1
aí eu faço por exemplo a letra a
a) AxB = {1,-2; 1,-1; 1,0; 1,1; 1,2}
e coloco eles no gráfico, certo isso?
-
Miya
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qui Mar 05, 2015 16:27
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Ter Mar 31, 2015 12:27
por adauto martins » Ter Mar 31, 2015 12:27
nao cara miya,
veja o intervalo,ou conjunto A,eh de numeros reais,entao entre (1,3) existem infinitos num.reais,assim tbem e o conj.B...vc esta os colocando como num.inteiros,e o problema diz
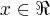
,q.eh uma propriedade dada no problema...logo o conj. de todos pares ordenados AXB,eh um retangulo contido no plano...o grafico aqui nao eh uma curva,e sim uma area,eh como vc desenhasse um retangulo,no sistema cartesiano e o colorisse... como vc esta os colocando(num.inteiros) ai sim seriam pontos no plano cartesiano...vc deve prestar sempre atençao na propriedade dada no conjunto...um conj. generico eh assim definido...seja A={

conj./x tem propriedade tal}...exemplo...seja A={plantas/as plantas sao arvores frutiferas}...e por ai...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [FUNÇÕES] PODEM ME AJUDAR POR FAVOR?
por Miya » Seg Abr 06, 2015 09:11
- 1 Respostas
- 1266 Exibições
- Última mensagem por adauto martins

Seg Abr 06, 2015 13:06
Funções
-
- Podem me ajudar...
por Fiel8 » Sáb Jun 27, 2009 20:00
- 1 Respostas
- 1575 Exibições
- Última mensagem por Molina

Seg Jun 29, 2009 20:50
Funções
-
- [questao IFRN geometria plana] sera que podem me ajudar
por kdeyse » Dom Jan 27, 2013 10:06
- 2 Respostas
- 1822 Exibições
- Última mensagem por kdeyse

Dom Jan 27, 2013 12:59
Geometria Plana
-
- Fatoração: por favor quem poder me ajudar
por ewerton220179 » Ter Nov 13, 2012 13:09
- 1 Respostas
- 2275 Exibições
- Última mensagem por Cleyson007

Ter Nov 13, 2012 14:06
Polinômios
-
- Alguem pode me ajudar neste exercício, por favor...
por caducustodio » Sex Ago 17, 2012 09:00
- 1 Respostas
- 1818 Exibições
- Última mensagem por Cleyson007

Sex Ago 17, 2012 09:50
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 ...eh o conjunto de todos os pares ordenadas (a,b)...aqui
...eh o conjunto de todos os pares ordenadas (a,b)...aqui 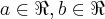 ,logo
,logo 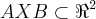 q. sera um quadrado no plano ,de lados 2 e 4...2=3-1,4=2-(-2)
q. sera um quadrado no plano ,de lados 2 e 4...2=3-1,4=2-(-2)

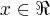 ,q.eh uma propriedade dada no problema...logo o conj. de todos pares ordenados AXB,eh um retangulo contido no plano...o grafico aqui nao eh uma curva,e sim uma area,eh como vc desenhasse um retangulo,no sistema cartesiano e o colorisse... como vc esta os colocando(num.inteiros) ai sim seriam pontos no plano cartesiano...vc deve prestar sempre atençao na propriedade dada no conjunto...um conj. generico eh assim definido...seja A={
,q.eh uma propriedade dada no problema...logo o conj. de todos pares ordenados AXB,eh um retangulo contido no plano...o grafico aqui nao eh uma curva,e sim uma area,eh como vc desenhasse um retangulo,no sistema cartesiano e o colorisse... como vc esta os colocando(num.inteiros) ai sim seriam pontos no plano cartesiano...vc deve prestar sempre atençao na propriedade dada no conjunto...um conj. generico eh assim definido...seja A={ conj./x tem propriedade tal}...exemplo...seja A={plantas/as plantas sao arvores frutiferas}...e por ai...
conj./x tem propriedade tal}...exemplo...seja A={plantas/as plantas sao arvores frutiferas}...e por ai...