" Vi uma resolução deste exercício, e nela, os coeficientes dos monômios de grau ímpar foram igualados a zero pelo motivo
de o polinômio ser uma função par. Não entendi o porquê disso, alguém poderia me ajudar? "
Nota : Uma função
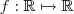
é ditar ser par ( respct . impar ) se

para todo x (respct .
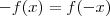
p/ todo x ) .
Seja

qualquer polinômio , i.e,
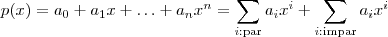
(a 1ª soma estende sobre todos índices pares compreendidos entre 0 e n e a 2ª sobre todos índices ímpares entre 0 e n ) .
Suponha p par , i.e , p(x) = p(-x) para todo x .Temos ,
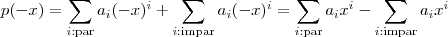
, logo
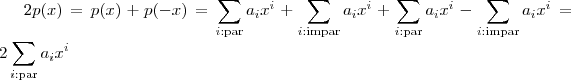
e assim o p(x) se resume a soma de todos os termos
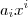
com índice par compreendidos entre 0 e n .
Caso p for impar , de forma análoga verifica-se que p(x) se exprime como soma de todos os termos
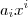
de índice
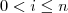
impar .
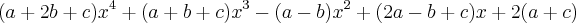 .
.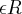 , é uma função par. Então, a soma dos módulos de suas raízes é igual a
, é uma função par. Então, a soma dos módulos de suas raízes é igual a![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
![\sqrt[2]{3} \sqrt[2]{3}](/latexrender/pictures/77529b271d4ed2ab8ca1f0755594aa28.png)
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)


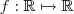 é ditar ser par ( respct . impar ) se
é ditar ser par ( respct . impar ) se  para todo x (respct .
para todo x (respct . 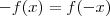 p/ todo x ) .
p/ todo x ) .  qualquer polinômio , i.e,
qualquer polinômio , i.e, 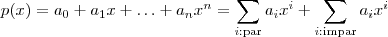
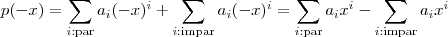 , logo
, logo 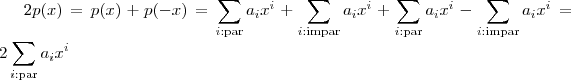
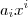 com índice par compreendidos entre 0 e n .
com índice par compreendidos entre 0 e n .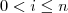 impar .
impar .