O gráfico de uma função g tem por assímptotas x =2 e y =5
Então o gráfico da função f , definida por f (x) =g(x +1)´- 2 tem por
assímptotas:



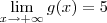 ; formalmente isso significa que para cada
; formalmente isso significa que para cada  que propormos existe um número
que propormos existe um número  correspondente ( ">>" para enfatizar que em geral ele está mt longe da origem) tal que se
correspondente ( ">>" para enfatizar que em geral ele está mt longe da origem) tal que se 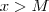 então a função
então a função  avaliada em
avaliada em  fica muito próximo de
fica muito próximo de  (
(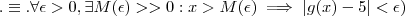 .
.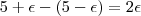 e base 'infinita' (
e base 'infinita' ( ![\{(x,g(x) ; x > M \} \subset [M,+\infty) \times [5-\epsilon , 5+\epsilon ] \{(x,g(x) ; x > M \} \subset [M,+\infty) \times [5-\epsilon , 5+\epsilon ]](/latexrender/pictures/ef9574ad537c80b89d95f4a98c02ef4a.png) ) .
) . 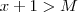 então
então ![| [g(x+1) -2] -3 | = |g(x+1) - 5 | < \epsilon | [g(x+1) -2] -3 | = |g(x+1) - 5 | < \epsilon](/latexrender/pictures/71173129b0bca055ee8700f4aa745eaf.png) , ou seja ,
, ou seja , 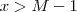 então
então 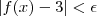 , logo a porção do gráfico de
, logo a porção do gráfico de  x > M-1 está dentro da caixa de altura mesma da caixa anterior e também base infinita (
x > M-1 está dentro da caixa de altura mesma da caixa anterior e também base infinita (![\{(x,f(x)) ; x > M - 1\} \subset [M-1,+\infty) \times [4-\epsilon , 4+\epsilon ] \{(x,f(x)) ; x > M - 1\} \subset [M-1,+\infty) \times [4-\epsilon , 4+\epsilon ]](/latexrender/pictures/3c7b8d34c07af78d3182ab95bebd5b17.png) )e muito mais que isso estamos dizendo formalmente que
)e muito mais que isso estamos dizendo formalmente que 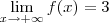 .
.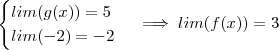 .
. 
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.



