Quais são os métodos possiveis para encontrarmos raizes de qualuqerr funções?
O método de Newton-Raphson não é perfeito mas é muito interessante.
Alguem poderia, por favor, enumerar outros métodos e se possivel com links com referencia?
1 - método de Newton-Raphson (para muitas funções) Não funciona, por exemplo, para
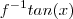
2 - baskara (para eq de 2º grau)
3 - Tartaglia (eq de 3º e 4º)


