 por silviopuc » Qui Dez 12, 2013 22:12
por silviopuc » Qui Dez 12, 2013 22:12
Boa noite,
Esse exercício eu não soube nem iniciar.
Se A é um conjunto não vazio então uma operação binária em A é uma função
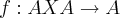
. Qual é o número de operações binárias em um conjunto A com p elementos?
a)

b)
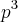
c)
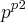
d)
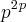
e)
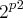
Gabarito: C
-
silviopuc
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Ter Jan 15, 2013 12:41
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Dez 13, 2013 00:01
por e8group » Sex Dez 13, 2013 00:01
Não tenho certeza se estar correto ,mas obtive como resposta
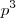
,de qualquer forma vou postar o que pensei .
Defina
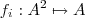
tal que para cada par ordenado em
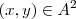
fixado, tem-se
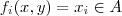
.Como
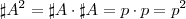
e para cada par ordenado (x,y) é possível definir

operações binárias em A ,então ao todo é possível definir
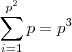
operações binárias em A .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Dez 18, 2013 22:45
por e8group » Qua Dez 18, 2013 22:45
Está errado . Sejam
conjuntos com respectivas cardinalidades
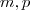
. Defina
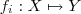
e mostremos que há
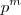
aplicações do conjunto

ao

.
Suponha
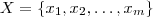
e
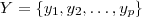
.
Veja o esquema a figura abaixo :

segmentos de retas verticais com as possíveis imagens pela aplicação :
Parti

(L_1) e chegar em

(em L_2) significar que é possível definir uma aplicação tal que

é levado a imagem

e

é levado a imagem

. Uma aplicação ficará bem determinada quando escolhemos um caminho que nos conecta de um ponto de
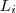
ao outro de
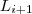
(i=1,... p-1) .
Objetivo migar de
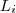
e
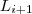
ao longo de
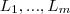
:
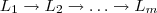
Partindo de

há

formas de chegar em

pelo que também há

maneiras de chegar em
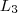
,..., e o mesmo para chegar em
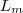
de
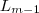
. Por estes esquema há

(p-vezes) de executar
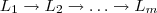
e portanto há
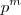
aplicações do conjunto

ao

.
Daí em particular para
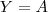
e
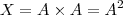
teremos
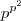
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dúvida,relação binária
por ibatexano » Sex Set 18, 2009 16:15
- 2 Respostas
- 5987 Exibições
- Última mensagem por ibatexano

Sex Set 18, 2009 23:14
Álgebra
-
- Relação binária
por MaiSantos » Sex Set 09, 2011 10:48
- 0 Respostas
- 1751 Exibições
- Última mensagem por MaiSantos

Sex Set 09, 2011 10:48
Funções
-
- Relação Binária
por abagadaia » Dom Dez 11, 2011 19:37
- 1 Respostas
- 2072 Exibições
- Última mensagem por abagadaia

Dom Dez 11, 2011 21:47
Álgebra Elementar
-
- Funções:Relação Binária
por +Julia » Sáb Abr 12, 2014 09:49
- 0 Respostas
- 2249 Exibições
- Última mensagem por +Julia

Sáb Abr 12, 2014 09:49
Funções
-
- Funções:Gráficos R e R-1 e Relação Binária
por +Julia » Sáb Abr 12, 2014 09:57
- 0 Respostas
- 2489 Exibições
- Última mensagem por +Julia

Sáb Abr 12, 2014 09:57
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
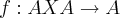 . Qual é o número de operações binárias em um conjunto A com p elementos?
. Qual é o número de operações binárias em um conjunto A com p elementos?
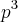
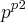
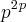
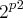

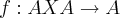 . Qual é o número de operações binárias em um conjunto A com p elementos?
. Qual é o número de operações binárias em um conjunto A com p elementos?
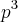
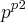
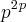
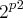

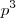 ,de qualquer forma vou postar o que pensei .
,de qualquer forma vou postar o que pensei . 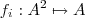 tal que para cada par ordenado em
tal que para cada par ordenado em 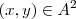 fixado, tem-se
fixado, tem-se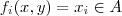 .Como
.Como 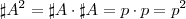 e para cada par ordenado (x,y) é possível definir
e para cada par ordenado (x,y) é possível definir  operações binárias em A ,então ao todo é possível definir
operações binárias em A ,então ao todo é possível definir 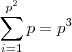 operações binárias em A .
operações binárias em A .
 conjuntos com respectivas cardinalidades
conjuntos com respectivas cardinalidades 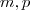 . Defina
. Defina 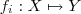 e mostremos que há
e mostremos que há 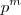 aplicações do conjunto
aplicações do conjunto  ao
ao  .
. 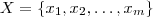 e
e 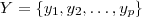 .
. segmentos de retas verticais com as possíveis imagens pela aplicação :
segmentos de retas verticais com as possíveis imagens pela aplicação : (L_1) e chegar em
(L_1) e chegar em  (em L_2) significar que é possível definir uma aplicação tal que
(em L_2) significar que é possível definir uma aplicação tal que  é levado a imagem
é levado a imagem  e
e  é levado a imagem
é levado a imagem  . Uma aplicação ficará bem determinada quando escolhemos um caminho que nos conecta de um ponto de
. Uma aplicação ficará bem determinada quando escolhemos um caminho que nos conecta de um ponto de 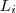 ao outro de
ao outro de 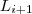 (i=1,... p-1) .
(i=1,... p-1) .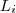 e
e 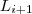 ao longo de
ao longo de 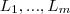 :
: 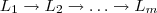
 há
há  formas de chegar em
formas de chegar em  pelo que também há
pelo que também há  maneiras de chegar em
maneiras de chegar em 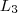 ,..., e o mesmo para chegar em
,..., e o mesmo para chegar em 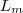 de
de 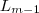 . Por estes esquema há
. Por estes esquema há  (p-vezes) de executar
(p-vezes) de executar 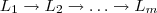 e portanto há
e portanto há 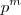 aplicações do conjunto
aplicações do conjunto  ao
ao  .
. 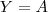 e
e 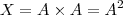 teremos
teremos 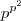 .
.