 por Victor985 » Qua Nov 13, 2013 10:07
por Victor985 » Qua Nov 13, 2013 10:07
Se
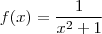
, quanto vale
![f (\sqrt[4]{7} f (\sqrt[4]{7}](/latexrender/pictures/eb2cfc9b327335e637053f65d31bfc81.png)
)?
Minha resolução:
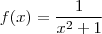
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png)
) =
![\frac {1}{(\sqrt[4]{7})^2 + 1} \frac {1}{(\sqrt[4]{7})^2 + 1}](/latexrender/pictures/b70755f8248de3cf19732baae2c75173.png)
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png)
) =
![\frac {1}{\sqrt[4]{7}^2 + 1} \frac {1}{\sqrt[4]{7}^2 + 1}](/latexrender/pictures/045ebbe707edff34a4244cd4a2c94c5a.png)
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png)
) =
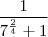
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png)
) =
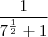
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png)
) =
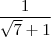
A partir daí, eu não soube mais como continuar.
Gabarito:
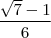
-
Victor985
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Sáb Nov 02, 2013 12:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Qua Nov 13, 2013 16:13
por e8group » Qua Nov 13, 2013 16:13
DIca :
Multiplique por
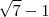
o numerador e denominador
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fuvest-SP
por luanxd » Dom Fev 07, 2010 20:16
- 4 Respostas
- 5417 Exibições
- Última mensagem por luanxd

Ter Fev 09, 2010 11:06
Sistemas de Equações
-
- Fuvest
por CaAtr » Sex Abr 02, 2010 16:39
- 5 Respostas
- 4646 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 14:27
Sistemas de Equações
-
- LOG FUVEST
por PHANIE » Ter Abr 12, 2011 13:22
- 1 Respostas
- 14739 Exibições
- Última mensagem por Molina

Ter Abr 12, 2011 15:13
Logaritmos
-
- FUVEST 1
 por PHANIE » Ter Abr 26, 2011 15:53
por PHANIE » Ter Abr 26, 2011 15:53
- 3 Respostas
- 14136 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:17
Geometria Plana
-
- fuvest 2
por PHANIE » Ter Abr 26, 2011 15:57
- 3 Respostas
- 5026 Exibições
- Última mensagem por FilipeCaceres

Qua Mai 04, 2011 12:33
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
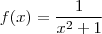 , quanto vale
, quanto vale ![f (\sqrt[4]{7} f (\sqrt[4]{7}](/latexrender/pictures/eb2cfc9b327335e637053f65d31bfc81.png) )?
)?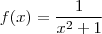
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png) ) =
) = ![\frac {1}{(\sqrt[4]{7})^2 + 1} \frac {1}{(\sqrt[4]{7})^2 + 1}](/latexrender/pictures/b70755f8248de3cf19732baae2c75173.png)
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png) ) =
) = ![\frac {1}{\sqrt[4]{7}^2 + 1} \frac {1}{\sqrt[4]{7}^2 + 1}](/latexrender/pictures/045ebbe707edff34a4244cd4a2c94c5a.png)
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png) ) =
) = 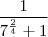
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png) ) =
) = 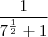
![f(\sqrt[4]{7} f(\sqrt[4]{7}](/latexrender/pictures/b56cd2872e34e04bef1233eab0e324c6.png) ) =
) = 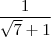
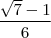

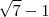 o numerador e denominador
o numerador e denominador


 , avisa que eu resolvo.
, avisa que eu resolvo.

