 por Thiago 86 » Seg Jul 15, 2013 18:46
por Thiago 86 » Seg Jul 15, 2013 18:46
Saudações estou estudando função modular e me deparei com essa questão:

Tentei fazer assim:
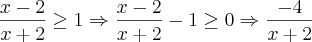
.Beleza! se encima tivesse outra icognita eu saberia responder fazendo f(x)/g(x), mas como não tem deu nó.
-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
 por Russman » Seg Jul 15, 2013 22:38
por Russman » Seg Jul 15, 2013 22:38
Voce começou de maneira correta. Note que,

na última relação que desenvolvemos o termo do numerador da fração é negativo e precisamos que o quociente seja positivo. Isso só acontece quando o denominador for negativo também, vista regra de sinais. Assim,

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Thiago 86 » Qua Jul 17, 2013 14:20
por Thiago 86 » Qua Jul 17, 2013 14:20
Valeu, eu me esqueci de repará nesse detalhe.

-
Thiago 86
- Usuário Dedicado

-
- Mensagens: 40
- Registrado em: Seg Fev 11, 2013 18:55
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso técnico em enfermagem
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2615 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3113 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
-
- Funçao modular
 por Skcedas » Qua Mai 26, 2010 19:29
por Skcedas » Qua Mai 26, 2010 19:29
- 6 Respostas
- 5366 Exibições
- Última mensagem por netlopes

Ter Jun 08, 2010 18:11
Funções
-
- Função Modular
 por DanieldeLucena » Seg Set 20, 2010 18:03
por DanieldeLucena » Seg Set 20, 2010 18:03
- 1 Respostas
- 2241 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:35
Funções
-
- Função Modular
por Pri Ferreira » Ter Nov 22, 2011 18:20
- 1 Respostas
- 1872 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 18:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

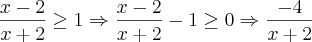 .Beleza! se encima tivesse outra icognita eu saberia responder fazendo f(x)/g(x), mas como não tem deu nó.
.Beleza! se encima tivesse outra icognita eu saberia responder fazendo f(x)/g(x), mas como não tem deu nó.

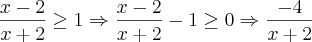 .Beleza! se encima tivesse outra icognita eu saberia responder fazendo f(x)/g(x), mas como não tem deu nó.
.Beleza! se encima tivesse outra icognita eu saberia responder fazendo f(x)/g(x), mas como não tem deu nó.

 .
.




 , avisa que eu resolvo.
, avisa que eu resolvo.

