Sugiro que vc escreva as funções e aí faça a maximização:
a) Receita é dada por p.x:
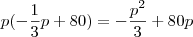
Para maximizar, vc precisa encontrar os pontos críticos e testar se é mínimo ou máximo. Pela forma da função, fica claro que será um máximo (é uma parábola côncava). Derivando e igualando a zero (ou seja, achando a função receita marginal):
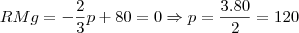
Basta resolver para p e substituir na equação de demanda:
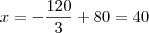
b) Lucro é RT - CT.
Basta substituir os valores de x: px - c(x) = 120.40 - 60.40-150 = 2250
c) A condição de lucro máximo é quando a RMg é igual ao CMg. Reescreva RMg em função de x.
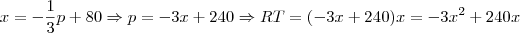

Para obter o custo marginal, da mesma forma que a receita, derive e iguale a zero a função custo. Aí basta igualar as duas funções e resolver para x:
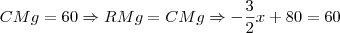
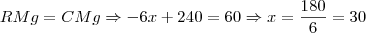
Com isso acho que dá pra concluir, certo?


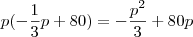
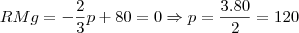
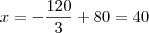
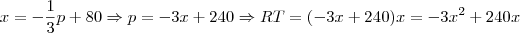

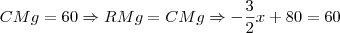
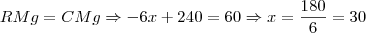

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.