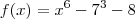
o resultado dela é 2 e -1.. eu consigo responder quando é elevado a quarta tipo essa:

que os zeros são 2, -1, 1 e -2..trocando o
 por outra incógnita tipo
por outra incógnita tipo 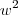 ..mas com
..mas com 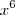 não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.
não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.

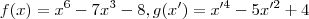 .Caso sejam ,podemos fazer
.Caso sejam ,podemos fazer 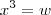 e
e  (Por quê ?) Assim ,
(Por quê ?) Assim ,  e
e  .
.
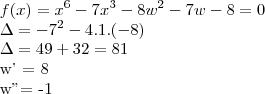
![{x}^{3} = 8
x = \sqrt[3]{8} = 2 {x}^{3} = 8
x = \sqrt[3]{8} = 2](/latexrender/pictures/b30ff66eecb340ed6150a37453d30c43.png)
![x = \sqrt[3]{-1} = 1 x = \sqrt[3]{-1} = 1](/latexrender/pictures/6c37998a534d7ac1ebce45e28aa97d5a.png) ? há alguma regra para índice ímpar com radicando -1 seja igual a 1?
? há alguma regra para índice ímpar com radicando -1 seja igual a 1?![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png) ,pois ,
,pois , 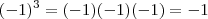 .Além disso ,
.Além disso ,  .Comente as dúvidas .
.Comente as dúvidas . é impar e o radicando
é impar e o radicando  é negativo ,o número é
é negativo ,o número é ![\sqrt[n]{a} < 0 \sqrt[n]{a} < 0](/latexrender/pictures/261ff9994999d43972a2ad6e6aa7238e.png) é real ,casso fosse
é real ,casso fosse ![\sqrt[n]{a} \notin \mathbb{R} \sqrt[n]{a} \notin \mathbb{R}](/latexrender/pictures/94826bbc3ed30a99672afbb1ec6cfacd.png) .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)