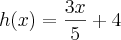por Jhennyfer » Qui Mai 16, 2013 12:07
por Jhennyfer » Qui Mai 16, 2013 12:07
Sejam f e g funções tais que
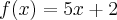
e

. Determine a lei que define a função afim h, sabendo que
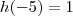
e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.
Não consegui nem iniciar a resolução =/
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Sex Mai 17, 2013 11:03
por Cleyson007 » Sex Mai 17, 2013 11:03
Bom dia Jhennyfer!
Vou te dar as dicas, ok? Qualquer dúvida me comunique

1°) Ache o
ponto de intersecção. Em outras palavras, faça
f(x) = g(x)2°) Substitua o valor de x (que você encontrou ao fazer o procedimento acima), e encontre y (que é o f(x)).
3°) Bom, uma função afim é do tipo y = ax +b. Substitua os valores de x e y na função acima (agora você terá uma equação com as incógnitas a e b).
4°) Volte a função afim (y = ax +b), agora vamos trabalhar o h(x)! h(-5) = 1
5°) A essas alturas você terá duas equações com a e b em cada uma, basta procurar os valores de a e b, respectivamente, e substituir os valores na função a fim y = ax +b.
Parece difícil, mas é tranquilo..
Att,
Cleyson
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Jhennyfer » Dom Mai 19, 2013 22:52
por Jhennyfer » Dom Mai 19, 2013 22:52
Oi Cleyson, boom....
eu fui seguindo os seus passos, e era a mesma coisa que eu estava fazendo, caio sempre na mesma coisa...
olha pra mim deu que
para f(x) x=-2/5 e y=0
para g(x) x=-7/6 e y=0
----------------------------------
peguei um dos pontos e substitui numa equação y=ax+b, e na segunda com os valores do ponto da função h.
resolvi o sistema e encontrei
a=27/5 e b=28.
tudo errado eu sei.
no gabarito está...
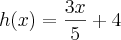
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Seg Mai 20, 2013 11:14
por Cleyson007 » Seg Mai 20, 2013 11:14
Bom dia Jhennyfer!
Escrevi a resolução passo-a-passo, escaneei, e estou te enviando..
Esteja a vontade para perguntar se surgirem dúvidas.
Segue resolução:

Atenciosamente,
Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Jhennyfer » Seg Mai 20, 2013 11:27
por Jhennyfer » Seg Mai 20, 2013 11:27
Vendo as minhas anotações... eu fui até o 3º passo e desisti achando q estava errado. Que raaiva!
Mas agora não restou nenhuma dúvida, obrigado!
-
Jhennyfer
- Usuário Parceiro

-
- Mensagens: 67
- Registrado em: Sáb Mar 30, 2013 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Cleyson007 » Seg Mai 20, 2013 11:41
por Cleyson007 » Seg Mai 20, 2013 11:41
Jhennyfer, fico feliz em saber que pude ajudar

Cleyson007
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função afim] Determinar a função afim
por Apprentice » Dom Set 30, 2012 21:49
- 4 Respostas
- 3232 Exibições
- Última mensagem por Apprentice

Seg Out 01, 2012 12:19
Funções
-
- funçao afim
por maiara amaral » Dom Mai 11, 2008 18:08
- 2 Respostas
- 4875 Exibições
- Última mensagem por Kabarosk

Sex Mai 29, 2015 01:45
Pedidos
-
- Funçao Afim
por thais silva » Qua Mai 19, 2010 17:30
- 3 Respostas
- 2989 Exibições
- Última mensagem por MarceloFantini

Seg Jul 12, 2010 22:04
Funções
-
- funçao afim
por emilly » Ter Ago 17, 2010 20:40
- 6 Respostas
- 7222 Exibições
- Última mensagem por emilly

Qui Ago 19, 2010 18:32
Funções
-
- Função Afim
por Kelvin Brayan » Ter Mai 31, 2011 01:59
- 1 Respostas
- 2931 Exibições
- Última mensagem por Kelvin Brayan

Ter Jun 07, 2011 16:29
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
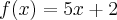 e
e  . Determine a lei que define a função afim h, sabendo que
. Determine a lei que define a função afim h, sabendo que 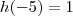 e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.
e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.
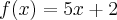 e
e  . Determine a lei que define a função afim h, sabendo que
. Determine a lei que define a função afim h, sabendo que 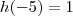 e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.
e que o gráfico de h passa pelo ponto de intersecção dos gráficos de f com g.