Eis o exercício:
Ache os pontos comuns aos gráficos das funções
 definida por
definida por 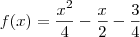 e sua inversa
e sua inversa  .
. Bom, tive que procurar na internet como achar a função inversa de uma função quadrática e cheguei a:
![f^{-1}(x)=1+2\,\sqrt[]{1+x} f^{-1}(x)=1+2\,\sqrt[]{1+x}](/latexrender/pictures/df79a0f240f347ce697636b8f9342ed6.png)
Daí igualei as duas funções, mas não consegui resolver por causa do x dentro da raiz.
Elevei os dois lados ao quadrado, mas também não obtive sucesso.
![x^2-2x-3=4(2\,\sqrt[]{1+x}) x^2-2x-3=4(2\,\sqrt[]{1+x})](/latexrender/pictures/937416660af8970b546849fb3406f141.png)
A resposta é:
![(3+2\,\sqrt[]{3}\,;\, 3+2\,\sqrt[]{3}) (3+2\,\sqrt[]{3}\,;\, 3+2\,\sqrt[]{3})](/latexrender/pictures/b28d4b6e8be5fe9cef452c287bcd928f.png)
Grata desde já!
Excelente final de semana!


 e
e  e sua função inversa.
e sua função inversa.
 .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.