 por thayna_rosa » Seg Nov 12, 2012 18:35
por thayna_rosa » Seg Nov 12, 2012 18:35
As coordenadas do ponto de máximo de uma função são (3,4).Sabendo que Um dos zeros desta função é igual a 5 , determine o outro zero da função.
-
thayna_rosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 12, 2012 18:28
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 19:57
por MarceloFantini » Seg Nov 12, 2012 19:57
Thayna, nosso objetivo não é resolver suas listas de exercício. O que você tentou? Podemos assumir que é uma parábola? Existem outras funções que satisfazem às condições do enunciado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por thayna_rosa » Seg Nov 12, 2012 19:59
por thayna_rosa » Seg Nov 12, 2012 19:59
esse é o problema não entendi o exercício
-
thayna_rosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 12, 2012 18:28
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por MarceloFantini » Seg Nov 12, 2012 20:43
por MarceloFantini » Seg Nov 12, 2012 20:43
Vamos assumir que seja uma parábola. Sendo assim, ela possui um ponto de máximo ou mínimo, dependendo da concavidade.
Um ponto de máximo significa que em qualquer outro valor a função assumirá um valor menor ou igual a este. De forma semelhante, um ponto de mínimo significa que em qualquer outro valor a função assumirá um valor maior ou igual a este.
A informação que

é um zero da função significa que
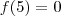
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por thayna_rosa » Seg Nov 12, 2012 20:58
por thayna_rosa » Seg Nov 12, 2012 20:58
ok ,obrigado.
-
thayna_rosa
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Nov 12, 2012 18:28
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equação Irracional] - Como desenvolver esse exercício?
por Crouff » Qui Jul 05, 2012 11:55
- 2 Respostas
- 1847 Exibições
- Última mensagem por Crouff

Qui Jul 05, 2012 12:29
Sistemas de Equações
-
- Fatoração - esse consegui desenvolver
por IsadoraLG » Qua Jul 09, 2014 21:47
- 1 Respostas
- 1088 Exibições
- Última mensagem por DanielFerreira

Qua Jul 16, 2014 20:41
Álgebra Elementar
-
- Quádricas não consigo desenvolver essa questão
por berg_nascimento » Qui Jun 30, 2016 14:58
- 0 Respostas
- 1462 Exibições
- Última mensagem por berg_nascimento

Qui Jun 30, 2016 14:58
Geometria Analítica
-
- Preciso de ajuda com esse exercício
por Dankaerte » Qui Set 10, 2009 19:10
- 2 Respostas
- 6296 Exibições
- Última mensagem por Elcioschin

Ter Abr 13, 2010 14:01
Matrizes e Determinantes
-
- ola poderiam me ajudar com esse exercicio de p.g
por willwgo » Qui Fev 24, 2011 17:09
- 3 Respostas
- 5030 Exibições
- Última mensagem por Lucas Ambrus de lima

Sáb Jun 29, 2013 21:47
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 é um zero da função significa que
é um zero da função significa que 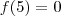 .
.



 .
.



