Em 1950, as populações de Toquio e de Nova Iorque eram de 7 e 12,6 milhões de habitantes, respectiva-
mente. Em 1974, as populações de Toquio e de Nova Iorque passaram para 20 e 16 milhões de habitantes,
respectivamente. Admitindo-se que o crescimento populacional dessas cidades foi linear no perodo 1950-
1974, determine o ano em que as duas cidades
ficaram com a mesma população.


 representa a quantidade de habitantes no ano
representa a quantidade de habitantes no ano  , então
, então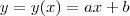 .
.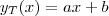 , e de Nova Iorque,
, e de Nova Iorque, 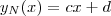 , e,com isso, reduzimos o problema a determinação das constantes
, e,com isso, reduzimos o problema a determinação das constantes  e
e  . Para simplificar as contas utilizarei a unidade de população
. Para simplificar as contas utilizarei a unidade de população 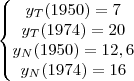
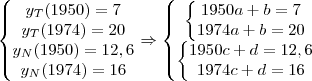 .
.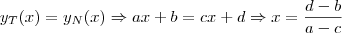 .
.

 .
.



