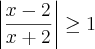
Minha resolução foi a seguinte:
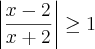
Para(I)
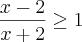
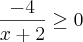
 cheguei nesse resultado
cheguei nesse resultadoColocando na reta real achei x < -2
Para(II)
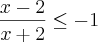
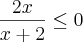
 cheguei nesse resultado
cheguei nesse resultadoColocando na reta real achei
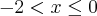
Fazendo a intersecção (I ? II) achei como solução S=

Resposta certa: {x ? ?|x?0 e x ? -2}


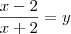 .
. , então
, então 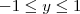 e portanto
e portanto 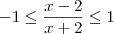 .
. 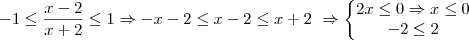
![S = (-\infty, -2)\cup (-2 ,0]= \left \{ x \in \mathbb{R} \setminus -2 \neq x \leq 0 \right \} S = (-\infty, -2)\cup (-2 ,0]= \left \{ x \in \mathbb{R} \setminus -2 \neq x \leq 0 \right \}](/latexrender/pictures/c46b9f026e79a7f913caeef4b33be544.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)