 por emsbp » Sáb Jun 30, 2012 17:46
por emsbp » Sáb Jun 30, 2012 17:46
Boa tarde.
O problema é o seguinte: «Admita que o carbono 14 sofre desintegração radioativa de acordo com a fórmula Q(t) =
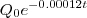
, com t medido em anos.
Uma amostra vegetal descoberta numa gruta pré-histórica contém apenas 20% do carbono 14 esperado em plantas vivas. Determine a idade aproximada da amostra.»
Ora, a meu ver, se a amostra apenas contém 20%, quer dizer que a desintegração foi de 80%. Logo Q(t)= 0.8. A questão é como vou determinar
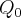
.
-
emsbp
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Sex Mar 09, 2012 11:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática/Informática
- Andamento: formado
 por MarceloFantini » Sáb Jun 30, 2012 21:48
por MarceloFantini » Sáb Jun 30, 2012 21:48
Estou imaginando que

represente a quantidade
restante de carbono no instante t. Pelo enunciado você sabe que resta apenas 20% do
inicial, significa que

. Agora faça
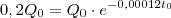
e encontre

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- funções exponenciais
por simas4387 » Qua Nov 24, 2010 16:40
- 1 Respostas
- 2054 Exibições
- Última mensagem por simas4387

Sex Dez 03, 2010 18:46
Funções
-
- [Funções Exponenciais]
por nicolascalcagnoto » Qua Set 07, 2011 20:29
- 21 Respostas
- 13233 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 16:00
Funções
-
- [Funções Exponenciais]
por nicolaspsy » Ter Set 20, 2011 02:05
- 1 Respostas
- 1822 Exibições
- Última mensagem por MarceloFantini

Qua Set 21, 2011 21:42
Funções
-
- Funcoes exponenciais
por Petrincha » Dom Jan 15, 2012 19:51
- 8 Respostas
- 4964 Exibições
- Última mensagem por Petrincha

Dom Jan 15, 2012 20:51
Funções
-
- [Funções exponenciais] Exercícios
por Texas » Qui Set 22, 2011 16:34
- 3 Respostas
- 2235 Exibições
- Última mensagem por MarceloFantini

Qui Set 22, 2011 19:23
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
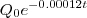 , com t medido em anos.
, com t medido em anos.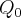 .
.

 represente a quantidade
represente a quantidade  . Agora faça
. Agora faça 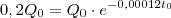 e encontre
e encontre  .
.
