por Jorge Salvino » Qui Abr 26, 2012 15:32
por Jorge Salvino » Qui Abr 26, 2012 15:32
Se [tex]{4}^{x}+4={2}^{x+2}[/tex], então o valor de[tex]2{x}^{2}+1[/tex] é igual a?
O QUE EU CONSEGUI?
Até agora eu fiz assim:
[tex]{4}^{x}+4={2}^{x+2}[/tex]
[tex]{4}^{x}+4 = {2}^{2} * {2}^{x}[/tex]
[tex]{2}^{2} = \frac{{4}^{x} + 4}{{2}^{x}}[/tex]
Depois daí eu não consegui fazer mais nada
-
Jorge Salvino
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 26, 2012 13:41
- Localização: Tianguá-Ce
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico Em Agricultura
- Andamento: cursando
-
 por DanielFerreira » Dom Abr 29, 2012 00:08
por DanielFerreira » Dom Abr 29, 2012 00:08
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Jorge Salvino » Dom Abr 29, 2012 20:24
por Jorge Salvino » Dom Abr 29, 2012 20:24
Muito Obrigado mesmo danjr5, eu já tinha procurado em outros fóruns, no Google e nada de conseguir a resposta.
Mais uma vez o meu muito obrigado!
-
Jorge Salvino
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 26, 2012 13:41
- Localização: Tianguá-Ce
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso Técnico Em Agricultura
- Andamento: cursando
-
 por DanielFerreira » Dom Abr 29, 2012 20:50
por DanielFerreira » Dom Abr 29, 2012 20:50
Não há de quê.
Até breve!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equacão um pouco complicada.
por gustavoluiss » Qua Nov 24, 2010 08:31
- 2 Respostas
- 1838 Exibições
- Última mensagem por davi_11

Qua Nov 24, 2010 12:44
Álgebra Elementar
-
- [P.A.]Com um pouco de matemática financeira
por lupaixao » Sex Jun 28, 2013 18:49
- 1 Respostas
- 2570 Exibições
- Última mensagem por young_jedi

Sáb Jun 29, 2013 21:10
Progressões
-
- [Álgebra Elementar] Se x=a.y/b, y=? Um pouco mais complicado
 por Zicra » Qua Mar 30, 2016 18:47
por Zicra » Qua Mar 30, 2016 18:47
- 4 Respostas
- 5060 Exibições
- Última mensagem por Zicra

Seg Abr 11, 2016 17:56
Álgebra Elementar
-
- que dificil
por giboia90 » Seg Abr 08, 2013 03:34
- 1 Respostas
- 1473 Exibições
- Última mensagem por anabatista

Ter Abr 09, 2013 01:37
Estatística
-
- Primitiva difícil
por photon » Sáb Set 19, 2009 18:39
- 0 Respostas
- 1451 Exibições
- Última mensagem por photon

Sáb Set 19, 2009 18:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


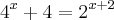 , então o valor de
, então o valor de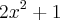 é igual a?
é igual a?
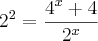
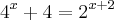
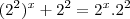
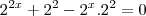
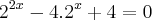
 :
: