Mostre que toda função definida em R (conjunto dos nros reais)
pode ser escrita como uma soma de uma função par com uma função ímpar.
Qual raciocínio tenho que usar para fazê-la?
Dei uma olhada nas aulas do Nerckie sobre o assunto, porém la mostra apenas a definição de tais função, assim como a forma de reconhecê-las graficamente.
preciso resolvê-la para hoje a tarde, se alguém puder ajudar-me...

estou lendo assuntos a respeito
se eu conseguir desenvolver o exercício volto aki e coloco pra vocês verem se está certo. Obrigada


 teremos que
teremos que 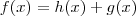 com
com  , que é par, e
, que é par, e  .
.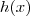 par e
par e  ímpar. Daí,
ímpar. Daí, 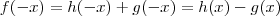 . Agora basta isolar
. Agora basta isolar 

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)