


ViniRFB escreveu:(ISS-NATAL - 2008 / ESAF) Uma função definida no conjunto dos números inteiros satisfaz a igualdade: f(x) - (x+1). f (Raiz quadrada de 2 - x) = Raiz Cúbica de x , para todo x inteiro. Com estas informações, conclui-se que f(0) é igual a:
Gabarito é - 2 elevado a -1/3.
ViniRFB escreveu:Peço desculpas que não sei usar o símbolos aqui ainda, mas eu tentei.
ViniRFB escreveu:Caríssimos minha primeira dúvida paira sobre essa função mesmo, propriamente dita, acredito que quando uma questão pede f(9) por exemplo, é que devemos substituir o 9 pela letra x, correto?
![f(x) - (x+1)f \left(\sqrt{2} - x\right) = \sqrt[3]{x} f(x) - (x+1)f \left(\sqrt{2} - x\right) = \sqrt[3]{x}](/latexrender/pictures/4ec0094aaf9a81bf05069e6f12ef5033.png)
![f(0) - (0+1)f \left(\sqrt{2} - 0\right) = \sqrt[3]{0} f(0) - (0+1)f \left(\sqrt{2} - 0\right) = \sqrt[3]{0}](/latexrender/pictures/c4aa1a75625678575d69781820ee3638.png)

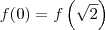
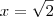 a função possui o mesmo valor.
a função possui o mesmo valor. não é um número inteiro. Sendo assim, não podemos substituir x por
não é um número inteiro. Sendo assim, não podemos substituir x por  na relação.
na relação. na relação:
na relação:![f\left(\sqrt{2}\right) - \left(\sqrt{2}+1\right)f \left(\sqrt{2} - \sqrt{2}\right) = \sqrt[3]{\sqrt{2}} f\left(\sqrt{2}\right) - \left(\sqrt{2}+1\right)f \left(\sqrt{2} - \sqrt{2}\right) = \sqrt[3]{\sqrt{2}}](/latexrender/pictures/3f9d5690b6755fc947e31cf0b9224f01.png)
![f\left(\sqrt{2}\right) - \left(\sqrt{2}+1\right)f \left(0\right) = \sqrt[6]{2} f\left(\sqrt{2}\right) - \left(\sqrt{2}+1\right)f \left(0\right) = \sqrt[6]{2}](/latexrender/pictures/647492661a6cfe3f25aa5d16b08c3ae6.png)
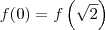 , podemos escrever que:
, podemos escrever que:![f(0) - \left(\sqrt{2}+1\right)f(0) = \sqrt[6]{2} f(0) - \left(\sqrt{2}+1\right)f(0) = \sqrt[6]{2}](/latexrender/pictures/c63b9cc953cd5026f39616fbdc2126e1.png)
![\left[1 - \left(\sqrt{2}+1\right)\right]f(0) = \sqrt[6]{2} \left[1 - \left(\sqrt{2}+1\right)\right]f(0) = \sqrt[6]{2}](/latexrender/pictures/455d004fa77e8b7e2f4ffd2b754a9fed.png)
![-\sqrt{2}f(0) = \sqrt[6]{2} -\sqrt{2}f(0) = \sqrt[6]{2}](/latexrender/pictures/ad1b64d356bfa28060c1c52c530f3206.png)
![f(0) = -\frac{\sqrt[6]{2}}{\sqrt{2}} f(0) = -\frac{\sqrt[6]{2}}{\sqrt{2}}](/latexrender/pictures/5c3865e6b9ca6db05b47e395d8c2a03c.png)
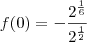
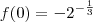




ViniRFB escreveu:N SEI USAR ESSAS FÓRMULAS. DESISTO


ViniRFB escreveu:Quero usá-las para explicar minhas dificuldades (...)
ViniRFB escreveu:(...) mas tem que ser um hiper cara para entender essas fórmulas (...)
ViniRFB escreveu:(...) ou estudar um tempão para poder postar (...)
ViniRFB escreveu:(...) daí atualmente não tenho esse time para ler entender e tal, pois o tempo que perco nessas fórmulas é algumas questões que deixo para trás (...)
ViniRFB escreveu:(...) Que coisa triste para mim, pois vocês os professores ajudam um monte a gente aqui, mas essas fórmulas complicam para expor às dúvidas.

 como uma distributiva ou não, se não como foi feita?
como uma distributiva ou não, se não como foi feita?
ViniRFB escreveu:f(0) - (0+1) = -1 ?
Se for esse valor -1 foi multiplicado porcomo uma distributiva ou não, se não como foi feita?
 é a mesma coisa que dizer que: multiplique o número -(0 + 1) pelo número
é a mesma coisa que dizer que: multiplique o número -(0 + 1) pelo número  .
. . Qual é o resultado disso? Ora, o resultado disso será simplesmente
. Qual é o resultado disso? Ora, o resultado disso será simplesmente 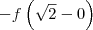 .
.


ViniRFB escreveu:Viu que coloquei as fórmulas?
ViniRFB escreveu:Peguei o tópico que me indicaste e imprimi assim vou vendo no papel enquanto digito.

 por que?
por que?
ViniRFB escreveu:por que?


ViniRFB escreveu:x-x = 0
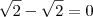 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.