 por Robinho » Seg Jan 16, 2012 12:09
por Robinho » Seg Jan 16, 2012 12:09
Alguem poderia me ajudar nessa questão aqui porfavor?
O produto (x-3).(x-4) é igual a
a) x²+12
b)x²-x+12
c)x²-12
e)x²-7x+12
Desde ja obrigado!!!
-
Robinho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 12:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Arkanus Darondra » Seg Jan 16, 2012 12:45
por Arkanus Darondra » Seg Jan 16, 2012 12:45
Olá Robinho,
Qual a sua dúvida neste exercício? Basta aplicar a propriedade distributiva
Exemplo:

e

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Robinho » Seg Jan 16, 2012 13:04
por Robinho » Seg Jan 16, 2012 13:04
Mas pelas contas que eu fiz deu o resultado da letra A
pelo menos confere pra mim se ta certo?
-
Robinho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 12:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Arkanus Darondra » Seg Jan 16, 2012 13:21
por Arkanus Darondra » Seg Jan 16, 2012 13:21
Tente identificar em que passo você errou.
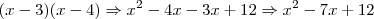
Qualquer dúvida...

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Robinho » Seg Jan 16, 2012 13:29
por Robinho » Seg Jan 16, 2012 13:29
Valeu acabei descobrino o que eu havia errado!!
Muito obrigado!
-
Robinho
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 12:15
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4946 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Produto Cos
por kryzay » Qui Fev 16, 2012 10:55
- 5 Respostas
- 2730 Exibições
- Última mensagem por MarceloFantini

Qui Fev 16, 2012 16:37
Trigonometria
-
- Produto
por Flavio Cacequi » Sáb Out 28, 2017 18:03
- 0 Respostas
- 1622 Exibições
- Última mensagem por Flavio Cacequi

Sáb Out 28, 2017 18:03
Aritmética
-
- Transformação em produto
 por Ananda » Seg Mar 24, 2008 17:31
por Ananda » Seg Mar 24, 2008 17:31
- 3 Respostas
- 5511 Exibições
- Última mensagem por Ananda

Ter Mar 25, 2008 14:55
Trigonometria
-
- Produto Cartesiano
por Cleyson007 » Seg Set 01, 2008 13:34
- 1 Respostas
- 7124 Exibições
- Última mensagem por admin

Seg Set 01, 2008 14:45
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e 


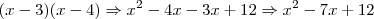





 , avisa que eu resolvo.
, avisa que eu resolvo.

