por Yasmin Felix » Sáb Jan 14, 2012 13:34
Renato sera que você poderia me ajudar nessa questão aqui por favor?
Quando a=3 , b=2 e c= -3 o valor numerico de
é igual a quanto?
Eu sei que é meio simples mais tem muito tempo que eu nao vejo isso ai agente acaba esquecendo!
Da pra você me dar uma ajudinha ?
-
Yasmin Felix
- Usuário Ativo
-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 13:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por Renato_RJ » Sáb Jan 14, 2012 14:05
Boa tarde Yasmin !!
Essa é bem simples, basta substituir os valores de a, b e c na equação, o que daria:
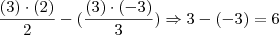
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-
Renato_RJ
- Colaborador Voluntário
-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
por Yasmin Felix » Sáb Jan 14, 2012 14:10
Valeu isso me ajudou muito e parabens você explica muito bem!!
-
Yasmin Felix
- Usuário Ativo
-
- Mensagens: 10
- Registrado em: Sáb Jan 14, 2012 13:28
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
por marques_gc » Sáb Jan 14, 2012 14:14
Resltado :
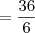
finalmente
-
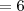
marques_gc
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Ter Nov 29, 2011 22:45
- Formação Escolar: SUPLETIVO
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3637 Exibições
- Última mensagem por DanielFerreira
Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- fração
por leandro moraes » Qui Jan 14, 2010 19:41
- 1 Respostas
- 1607 Exibições
- Última mensagem por MarceloFantini
Qui Jan 14, 2010 20:09
Estatística
-
- Fração
por bia rosendo » Seg Jun 06, 2011 11:45
- 2 Respostas
- 4392 Exibições
- Última mensagem por Claudin
Seg Jun 06, 2011 18:34
Matemática Financeira
-
- Fração 110
por Raphael Feitas10 » Seg Jan 09, 2012 17:28
- 1 Respostas
- 1757 Exibições
- Última mensagem por Arkanus Darondra
Seg Jan 09, 2012 18:43
Sistemas de Equações
-
- Fração 112
por Raphael Feitas10 » Sex Jan 13, 2012 02:23
- 1 Respostas
- 1578 Exibições
- Última mensagem por ant_dii
Sex Jan 13, 2012 03:18
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
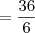
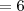
