 por Adriana Barbosa » Ter Mai 26, 2009 23:39
por Adriana Barbosa » Ter Mai 26, 2009 23:39
Dado um pedaço de papelão quadrado com 8 cm de lado, tira-se de cada canto do papelão, quadrados com x cm de lados e os bordos são dobrados de modo que forme uma caixa sem tampa. Determine:
(a) O volume V da caixa em função de x;
(b) A área S da caixa em função de x.
Por favor poderia me dizer algumas dicas de como poderia resolver esta questão?
Estou sem

!
Por favor me ajude!

-
Adriana Barbosa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 26, 2009 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Ter Mai 26, 2009 23:55
por Molina » Ter Mai 26, 2009 23:55
Primeiramente vamos tentar resolver a letra a)
Sugiro que você monte um esboço do que o problema quer. Você já conseguiu interpretá-lo?
Depois disso, você precisa usar o volume de um paralelepípedo, que é:
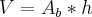
, onde
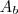
é a área da base e

é a altura.
Experimente pegar x como 1, 2, 3 e veja qual resultado quer. Pegar x como esses valores, significa que você irá cortar nas pontas um quadrado de lado 1, 2 e 3 e irá sobrar as partes que sobraram, formando, como o enunciado diz, uma caixa sem tampa.
Tente aí e depois me diga onde você chegou..
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adriana Barbosa » Qua Mai 27, 2009 00:23
por Adriana Barbosa » Qua Mai 27, 2009 00:23
Ainda não estou conseguindo!
Criei um esboço, se seria desta forma que estou pensando! Esta anexado no arquivo!
Obrigada, pela atenção e pela paciência!
- Anexos
-
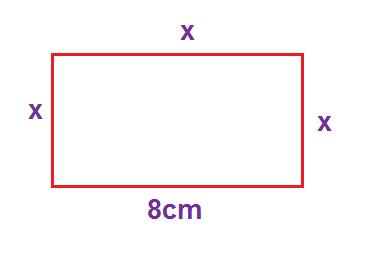
- esboço, matemática.jpg (5.69 KiB) Exibido 2476 vezes
-
Adriana Barbosa
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 26, 2009 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por Molina » Qua Mai 27, 2009 00:46
por Molina » Qua Mai 27, 2009 00:46
Fiz uma nova figura para ve se voce visualiza melhor.
Tente entender o valor que eu coloquei a cada lado.
A área pintada de cinza significa a área da base. Quanto ela vale?
Boas tentativas,

- Anexos
-
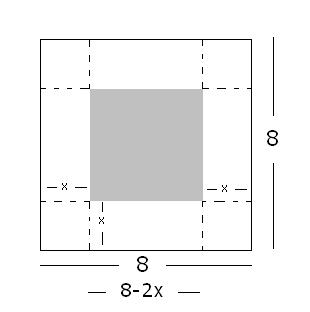
- caixa.JPG (8.14 KiB) Exibido 2471 vezes
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função real definida pela soma de uma função par c/uma ímpar
por Taah » Sáb Mar 27, 2010 15:33
- 3 Respostas
- 5583 Exibições
- Última mensagem por Taah

Dom Mar 28, 2010 13:21
Funções
-
- [plano tangente a função de duas variaveis dada por função]
por isaac naruto » Qui Dez 31, 2015 16:35
- 0 Respostas
- 4592 Exibições
- Última mensagem por isaac naruto

Qui Dez 31, 2015 16:35
Cálculo: Limites, Derivadas e Integrais
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5751 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- +uma função das trevas.ajuda aew!(função par mas heim!?)
por Fabricio dalla » Dom Fev 27, 2011 16:12
- 2 Respostas
- 3490 Exibições
- Última mensagem por LuizAquino

Dom Mar 06, 2011 09:17
Funções
-
- [FUNÇÃO] Não consigo achar a fórmula da função
por LAZAROTTI » Qui Set 27, 2012 00:06
- 1 Respostas
- 2958 Exibições
- Última mensagem por MarceloFantini

Qui Set 27, 2012 07:13
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 !
!

 !
!

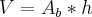 , onde
, onde 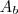 é a área da base e
é a área da base e  é a altura.
é a altura.



![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.